题目内容
在Rt 中,
中, ( )
( )
A.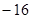 | B.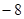 | C.8 | D.16 |
D
解析试题分析:根据题意,由于在Rt 中,
中,  AC的长度乘以AB在AC上的投影的积,那么结合向量的数量积的几何意义可知为
AC的长度乘以AB在AC上的投影的积,那么结合向量的数量积的几何意义可知为 =16,故答案为D.
=16,故答案为D.
考点:向量的数量积
点评:主要是考查了向量的数量积的运算,属于基础题。

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
对于任意向量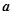 、
、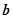 、
、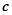 ,下列命题中正确的是 ( )
,下列命题中正确的是 ( )
A.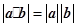 | B.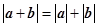 | C.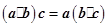 | D.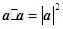 |
已知非零向量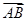 与
与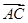 满足
满足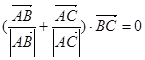 且
且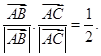 则
则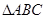 为( )
为( )
| A.等边三角形 | B.直角三角形 |
| C.等腰非等边三角形 | D.三边均不相等的三角形 |
若 且
且 与
与 也互相垂直,则
也互相垂直,则 的值为 ( )
的值为 ( )
A.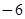 | B. | C.3 | D.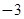 |
如图直角三角形 中,
中, ,
, ,点
,点 ,
, 分别在
分别在 ,
, 上,且
上,且 ,
, ,则
,则 ( )
( ) 
A. | B. | C. | D. |
已知向量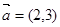 ,
,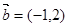 ,若
,若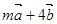 与
与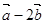 共线,则 ( )
共线,则 ( )
A. | B. | C.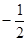 | D.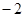 |
已知向量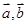 满足
满足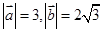 ,且
,且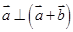 ,则
,则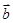 在
在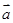 方向上的投影为( )
方向上的投影为( )
| A.3 | B.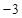 . . | C. | D.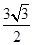 |
平面向量的集合 到
到 的映射
的映射 ,其中
,其中 为常向量.若映射
为常向量.若映射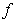 满足
满足 对任意的
对任意的 恒成立,则
恒成立,则 的坐标可能是( )
的坐标可能是( )
A.( , , ) ) | B.( , , ) ) | C.( , , ) ) | D.( , , ) ) |
若向量方程2x-3(x-2a)=0,则向量x等于( )
A. a a | B.-6a | C.6a | D.- a a |