题目内容
已知圆台上、下底面圆周都在球面上，且下底面过球心，母线与底面所成的角为| π | 3 |
分析：设出球的半径，求出圆台上底面半径，圆台的高，求出圆台体积，球的体积即可．
解答：解：设球的半径为2，由题意可得圆台上底面半径为1，
圆台的高为
，所以圆台的体积是：
πh(R2+r2+rR) =
球的体积：
πR3=
圆台的体积与球体积之比为：
故答案为：
圆台的高为
| 3 |
| 1 |
| 3 |
7
| ||
| 3 |
球的体积：
| 4 |
| 3 |
| 32π |
| 3 |
圆台的体积与球体积之比为：
7
| ||
| 32 |
故答案为：
7
| ||
| 32 |
点评：本题考查球的体积和表面积，棱柱、棱锥、棱台的体积，考查计算能力，逻辑思维能力，是基础题．
练习册系列答案
全优测试卷系列答案
冲刺100分1号卷系列答案
相关题目
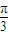，则圆台的体积与球体积之比为 ．
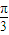，则圆台的体积与球体积之比为 ．