题目内容
已知椭圆E: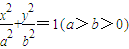 的离心率为
的离心率为 ,右焦点为F,且椭圆E上的点到点F距离的最小值为2.
,右焦点为F,且椭圆E上的点到点F距离的最小值为2.(1)求椭圆E的方程;
(2)设椭圆E的左、右顶点分别为A,B,过点A的直线l与椭圆E及直线x=8分别相交于点M,N.
(ⅰ)当过A,F,N三点的圆半径最小时,求这个圆的方程;
(ⅱ)若
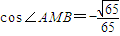 ,求△ABM的面积.
,求△ABM的面积.
【答案】分析:(1)由离心率为 ,椭圆E上的点到点F距离的最小值为2,即a-c=2联立方程组求a,c的值,然后利用b2=a2-c2求出b2,则椭圆方程可求;
,椭圆E上的点到点F距离的最小值为2,即a-c=2联立方程组求a,c的值,然后利用b2=a2-c2求出b2,则椭圆方程可求;
(2)(ⅰ)设出圆的一般方程,设N(8,t),把三点A(-4,0),F(2,0),N(8,t)代入圆的方程整理成标准式后利用基本不等式求出半径的最小值,同时求得半径最小时的圆的方程;
(ⅱ)设出直线l的方程,和椭圆方程联立后利用根与系数关系求出M点的坐标,由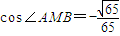 ,借助于向量数量积求出直线的斜率,进一步得到M点的纵坐标,则△ABM的面积可求.
,借助于向量数量积求出直线的斜率,进一步得到M点的纵坐标,则△ABM的面积可求.
解答:解:(1)由已知,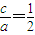 ,且a-c=2,所以a=4,c=2,所以b2=a2-c2=12,
,且a-c=2,所以a=4,c=2,所以b2=a2-c2=12,
所以椭圆E的方程为 .
.
(2)(ⅰ)由(1),A(-4,0),F(2,0),设N(8,t).
设圆的方程为x2+y2+dx+ey+f=0,将点A,F,N的坐标代入,得
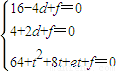 ,解得
,解得 .
.
所以圆的方程为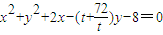 ,
,
即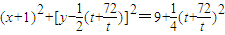 ,
,
因为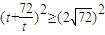 ,当且仅当
,当且仅当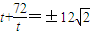 时,圆的半径最小,
时,圆的半径最小,
故所求圆的方程为 .
.
(ⅱ)由对称性不妨设直线l的方程为y=k(x+4)(k>0).
由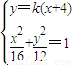 ,得(3+4k2)x2+32k2x+64k2-48=0
,得(3+4k2)x2+32k2x+64k2-48=0
由-4+xM= ,得
,得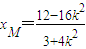 ,所以
,所以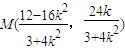 ,
,
所以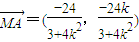 ,
, ,
,
所以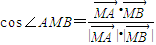 =
=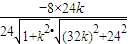 =
= ,
,
化简,得16k4-40k2-9=0,
解得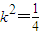 ,或
,或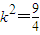 ,即
,即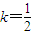 ,或
,或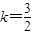 ,
,
此时总有yM=3,所以△ABM的面积为 .
.
点评:本题考查了圆与椭圆的标准方程,考查了直线与圆锥曲线的关系,直线与圆锥曲线联系在一起的综合题在高考中多以高档题、压轴题出现,主要涉及位置关系的判定,弦长问题、最值问题、对称问题、轨迹问题、面积问题等.突出考查了数形结合、分类讨论、函数与方程、等价转化等数学思想方法.属难题.
 ,椭圆E上的点到点F距离的最小值为2,即a-c=2联立方程组求a,c的值,然后利用b2=a2-c2求出b2,则椭圆方程可求;
,椭圆E上的点到点F距离的最小值为2,即a-c=2联立方程组求a,c的值,然后利用b2=a2-c2求出b2,则椭圆方程可求;(2)(ⅰ)设出圆的一般方程,设N(8,t),把三点A(-4,0),F(2,0),N(8,t)代入圆的方程整理成标准式后利用基本不等式求出半径的最小值,同时求得半径最小时的圆的方程;
(ⅱ)设出直线l的方程,和椭圆方程联立后利用根与系数关系求出M点的坐标,由
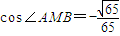 ,借助于向量数量积求出直线的斜率,进一步得到M点的纵坐标,则△ABM的面积可求.
,借助于向量数量积求出直线的斜率,进一步得到M点的纵坐标,则△ABM的面积可求.解答:解:(1)由已知,
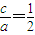 ,且a-c=2,所以a=4,c=2,所以b2=a2-c2=12,
,且a-c=2,所以a=4,c=2,所以b2=a2-c2=12,所以椭圆E的方程为
 .
.(2)(ⅰ)由(1),A(-4,0),F(2,0),设N(8,t).
设圆的方程为x2+y2+dx+ey+f=0,将点A,F,N的坐标代入,得
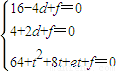 ,解得
,解得 .
.所以圆的方程为
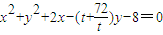 ,
,即
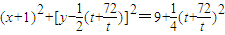 ,
,因为
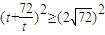 ,当且仅当
,当且仅当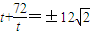 时,圆的半径最小,
时,圆的半径最小,故所求圆的方程为
 .
.(ⅱ)由对称性不妨设直线l的方程为y=k(x+4)(k>0).
由
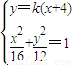 ,得(3+4k2)x2+32k2x+64k2-48=0
,得(3+4k2)x2+32k2x+64k2-48=0由-4+xM=
 ,得
,得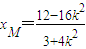 ,所以
,所以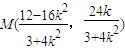 ,
,所以
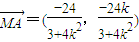 ,
, ,
,所以
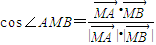 =
=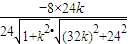 =
= ,
,化简,得16k4-40k2-9=0,
解得
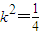 ,或
,或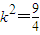 ,即
,即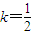 ,或
,或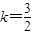 ,
,此时总有yM=3,所以△ABM的面积为
 .
.点评:本题考查了圆与椭圆的标准方程,考查了直线与圆锥曲线的关系,直线与圆锥曲线联系在一起的综合题在高考中多以高档题、压轴题出现,主要涉及位置关系的判定,弦长问题、最值问题、对称问题、轨迹问题、面积问题等.突出考查了数形结合、分类讨论、函数与方程、等价转化等数学思想方法.属难题.

练习册系列答案
 阳光课堂课时作业系列答案
阳光课堂课时作业系列答案
相关题目
 的离心率为
的离心率为 ,左焦点为F,过原点的直线l交椭圆于M,N两点,△FMN面积的最大值为1.
,左焦点为F,过原点的直线l交椭圆于M,N两点,△FMN面积的最大值为1. .
.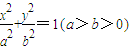 的离心率为
的离心率为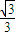 ,它的上顶点为A,左、右焦点分别为F1,F2,直线AF1,AF2分别交椭圆于点B,C.
,它的上顶点为A,左、右焦点分别为F1,F2,直线AF1,AF2分别交椭圆于点B,C.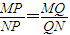 ,试证明点Q恒在一定直线上.
,试证明点Q恒在一定直线上.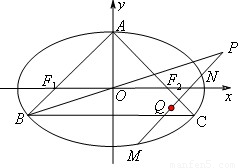
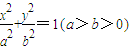 的离心率
的离心率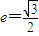 ,A1,A2分别是椭圆E的左、右两个顶点,圆A2的半径为a,过点A1作圆A2的切线,切点为P,在x轴的上方交椭圆E于点Q.
,A1,A2分别是椭圆E的左、右两个顶点,圆A2的半径为a,过点A1作圆A2的切线,切点为P,在x轴的上方交椭圆E于点Q.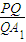 的值;
的值;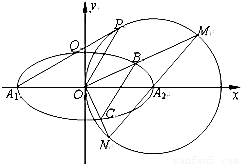
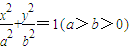 的离心率为
的离心率为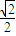 ,且过点
,且过点 ,设椭圆的右准线l与x轴的交点为A,椭圆的上顶点为B,直线AB被以原点为圆心的圆O所截得的弦长为
,设椭圆的右准线l与x轴的交点为A,椭圆的上顶点为B,直线AB被以原点为圆心的圆O所截得的弦长为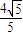 .
. 为定值;且当M在直线l上运动时,点Q在一个定圆上.
为定值;且当M在直线l上运动时,点Q在一个定圆上.
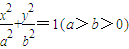 的离心率为
的离心率为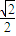 ,且过点
,且过点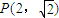 ,设椭圆的右准线l与x轴的交点为A,椭圆的上顶点为B,直线AB被以原点为圆心的圆O所截得的弦长为
,设椭圆的右准线l与x轴的交点为A,椭圆的上顶点为B,直线AB被以原点为圆心的圆O所截得的弦长为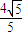 .
.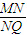 为定值;且当M在直线l上运动时,点Q在一个定圆上.
为定值;且当M在直线l上运动时,点Q在一个定圆上.