题目内容
【题目】![]() 已知点F为抛物线E:
已知点F为抛物线E:![]() 的焦点,点A(2,m)在抛物线E上,且|AF|=3
的焦点,点A(2,m)在抛物线E上,且|AF|=3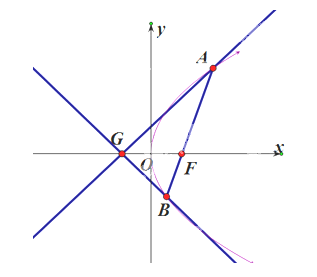 .
.
(1)求抛物线E的方程;
(2)已知点G(-1,0) , 延长AF交抛物线E于点B , 证明:以点F为圆心且与直线GA相切的圆,必与直线GB相切.
【答案】
(1)
![]()
(2)
详见解析
【解析】解法一:(1)由抛物线的定义得|AF|=2+![]() .因为|AF|=3,即2+
.因为|AF|=3,即2+![]() =3,解得p=2,所以抛物线E的方程为
=3,解得p=2,所以抛物线E的方程为![]() =4x。
=4x。
(2)因为点A(2,m)在抛物线E:![]() =4x上,所以m=
=4x上,所以m=![]() ,由抛物线的对称性,不妨设A(2,
,由抛物线的对称性,不妨设A(2,![]() ). 由A(2,
). 由A(2,![]() ),F(1,0)得直线AF的方程式为y=
),F(1,0)得直线AF的方程式为y=![]() (x-1)。 由
(x-1)。 由![]() ,得
,得![]() , 解得x=2或x=
, 解得x=2或x=![]() ,从而B(
,从而B(![]() ,-
,-![]() ),又G(-1,0),所以
),又G(-1,0),所以![]() ,所以
,所以![]() +
+![]() =0,从而
=0,从而![]() AGF=
AGF=![]() BGF,这表明点F到直线GA,GB的距离相等。故以F为圆心且与直线GA相切的圆必与直线GB相切。
BGF,这表明点F到直线GA,GB的距离相等。故以F为圆心且与直线GA相切的圆必与直线GB相切。
解法二:(1)同解法一。
(2)设以点F为圆心且与直线GA相切的圆的半径为r。 因为点A(2,m)在抛物线E:![]() =4x上,所以m=
=4x上,所以m=![]() ,由抛物线的对称性,不妨设A(2,
,由抛物线的对称性,不妨设A(2,![]() ). 由A(2,
). 由A(2,![]() ),F(1,0)得直线AF的方程式为y=
),F(1,0)得直线AF的方程式为y=![]() (x-1)。 由
(x-1)。 由![]() ,得
,得![]() , 解得x=2或x=
, 解得x=2或x=![]() ,从而B(
,从而B(![]() ,-
,-![]() ),又G(-1,0),故直线GA的方程式为
),又G(-1,0),故直线GA的方程式为![]() ,从而
,从而![]() ,又GB的方程式为
,又GB的方程式为![]() ,所以点F到直线,GB的距离
,所以点F到直线,GB的距离![]() ,这表明以点F为圆心且与直线GA相切的圆必与直线GB相切。
,这表明以点F为圆心且与直线GA相切的圆必与直线GB相切。

练习册系列答案
 初中学业考试导与练系列答案
初中学业考试导与练系列答案
相关题目
