Question

一个球与上底面边长为4，下底面边长为8的正四棱台各面都相切，则球的体积与正四棱台的体积之比为

[　　]

A．π∶6

B．π∶7

C．π∶8

D．π∶9

Answer 1

答案：B
解析：

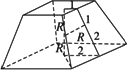
如图所示，设内切球半径为R，由球与正四棱台各面都相切，可得R2＋4＋R2＋16＝(4＋2)2，解得R＝2，则V球∶V正四棱台＝πR3∶×(16＋4×8＋64)×2R＝π∶7，故应选B．