题目内容
已知 的一个内角为120o,并且三边长构成公差为4的等差数列,则
的一个内角为120o,并且三边长构成公差为4的等差数列,则 的面积为_______________
的面积为_______________
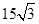
解析试题分析:设三角形的三边长为a-4,b=a,c=a+4,(a<b<c),根据题意可知三边长构成公差为4的等差数列,可知a+c="2b" ,C="120"  ,,则由余弦定理,c
,,则由余弦定理,c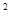 = a
= a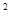 + b
+ b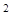 -2abcosC,
-2abcosC,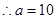 ,s三边长为6,10,14,,b
,s三边长为6,10,14,,b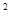 = a
= a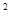 + c
+ c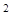 -2accosB,即
-2accosB,即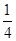 (a+c)
(a+c)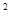 =a
=a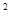 +c
+c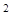 -2accosB, cosB=
-2accosB, cosB=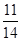 ,sinB=
,sinB=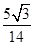 可知S=
可知S=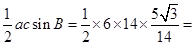 =
=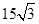 .
.
考点:本试题主要考查了等差数列与解三角形的面积的求解的综合运用。
点评:解决该试题的关键是利用余弦定理来求解,以及边角关系的运用,正弦面积公式来求解。巧设变量a-4,a,a+4会简化运算。

练习册系列答案
相关题目
 的最大值为_________.
的最大值为_________. 的解的个数为__________.
的解的个数为__________. 的图象如图所示,则
的图象如图所示,则 的解析式是__________________
的解析式是__________________ 
 ,
, ,且
,且 ,其中
,其中 .
. 和
和 的值;
的值; ,
, ,求角
,求角 的值.
的值. 为锐角,若
为锐角,若 ,则
,则 的值为 .
的值为 . +cos2α=_________________.
+cos2α=_________________. ,现有下列命题:
,现有下列命题: 是偶函数;
是偶函数; ;
; 是函数
是函数 上单调递增,在区间
上单调递增,在区间 上单调递减。
上单调递减。 ,则行列式
,则行列式