题目内容
甲、乙两个箱子中装有大小相同的小球,甲箱中有2个红球和2个黑球,乙箱中装有2个黑球和3个红球,现从甲箱和乙箱中各取一个小球并且交换.
(1)求交换后甲箱中刚好有两个黑球的概率.
(2)设交换后甲箱中黑球的个数为ξ,求ξ的分布列和数学期望.
(1)求交换后甲箱中刚好有两个黑球的概率.
(2)设交换后甲箱中黑球的个数为ξ,求ξ的分布列和数学期望.
分析:(1)事件“交换后甲盒中恰有2个黑球”可以分解为①取出的两个球都是黑球;②取出的两个球都是红球,因此按这两种情况分类讨论分别求出相应的概率,最后用概率的加法公式,即可得出所要求的概率;
(2)ξ的可能取值为1,2,3,分别求出P(ξ=1),P(ξ=2),P(ξ=3),由此能求出ξ的分布列和数学期望.
(2)ξ的可能取值为1,2,3,分别求出P(ξ=1),P(ξ=2),P(ξ=3),由此能求出ξ的分布列和数学期望.
解答:解:甲乙两盒各取一个球交换后,甲盒中恰有2个黑球有下面几种情况:
①取出的两个球都是黑球,则甲盒恰好有2个黑球的事件记为A1,
则P(A1)=
=
.
②取出的两个球都是红球,则此时甲盒中恰有2个黑球的事件记为A2,
则P(A2)=
=
.(6分)
故P1=P(A1)+P(A2)=
+
=
.
(2)ξ的可能取值为1,2,3,
P(ξ=1)=
=
,
P(ξ=2)=
,
P(ξ=3)=
=
.
∴ξ的分布列为:
∴Eξ=1×
+2×
+3×
=
.
①取出的两个球都是黑球,则甲盒恰好有2个黑球的事件记为A1,
则P(A1)=
| ||||
|
| 1 |
| 5 |
②取出的两个球都是红球,则此时甲盒中恰有2个黑球的事件记为A2,
则P(A2)=
| ||||
|
| 3 |
| 10 |
故P1=P(A1)+P(A2)=
| 1 |
| 5 |
| 3 |
| 10 |
| 1 |
| 2 |
(2)ξ的可能取值为1,2,3,
P(ξ=1)=
| ||||
|
| 3 |
| 10 |
P(ξ=2)=
| 1 |
| 2 |
P(ξ=3)=
| ||||
|
| 1 |
| 5 |
∴ξ的分布列为:
| ξ | 1 | 2 | 3 | ||||||
| P |
|
|
|
| 3 |
| 10 |
| 1 |
| 2 |
| 1 |
| 5 |
| 19 |
| 10 |
点评:本题着重考查了等可能事件的概率、离散型随机变量及其分布列和离散型随机变量的期望与方差等知识点,属于中档题.请同学们注意解题过程中事件分解的思路和公式的正确使用.

练习册系列答案
相关题目
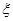 ,求
,求