题目内容
11.在钝角三角形ABC中,A,B,C的对边分别是a,b,c,B=60°,4sinC-6sinA=$\sqrt{3}$,则$\frac{c}{a}$=$\frac{17}{12}$.分析 利用已知可得2$\sqrt{3}$cosA-4sinA=$\sqrt{3}$①,由sinA>0,可得cosA>0,即A为锐角,C为钝角,又sin2A+cos2A=1②,由①②可解得sinA,可求sinC,由正弦定理即可得解.
解答 解:∵B=60°,4sinC-6sinA=$\sqrt{3}$,
∴4sin(120°-A)-6sinA=2$\sqrt{3}$cosA-4sinA=$\sqrt{3}$①,
∵sinA>0,故由①可得cosA>0,即A为锐角,C必然为钝角.
又∵sin2A+cos2A=1②,
∴由①②可解得:7sin2A+2$\sqrt{3}$sinA-$\frac{9}{4}$=0.解得:sinA=$\frac{3\sqrt{3}}{14}$.
∴sinC=$\frac{\sqrt{3}+6sinA}{4}$=$\frac{4\sqrt{3}}{7}$,
∴由正弦定理可得:$\frac{c}{a}=\frac{sinC}{sinA}$=$\frac{8}{3}$.
故答案为:$\frac{8}{3}$.
点评 本题主要考查了正弦定理,两角差的正弦函数公式,同角三角函数关系式的应用,考查了计算能力,属于中档题.

练习册系列答案
相关题目
2.已知tanα,tanβ为方程x2-5x+2=0的解,则tan(α+β)的值为( )
| A. | $\frac{1}{5}$ | B. | 5 | C. | -5 | D. | -1 |
6.不等$\frac{1}{a-b}+\frac{1}{b-c}+\frac{λ}{c-a}<0$对满足a>b>c恒成立,则λ的取值范围 ( )
| A. | (-∞,0] | B. | (-∞,1) | C. | (-∞,4] | D. | (4,+∞) |
16.已知命题p:?x∈[-1,2],函数f(x)=x2-x的值大于0,若p∨q是真命题,则命题q可以是( )
| A. | ?x∈(-1,1)使得cosx<$\frac{1}{2}$ | |
| B. | “-3<m<0”是“函数f(x)=x+log2x+m在区间($\frac{1}{2}$,2)上有零点”的必要不充分条件 | |
| C. | x=$\frac{π}{6}$是曲线f(x)=$\sqrt{3}$sin2x+cos2x的一条对称轴 | |
| D. | 若x∈(0,2),则在曲线f(x)=ex(x-2)上任意一点处的切线的斜率不小于-$\frac{1}{e}$ |

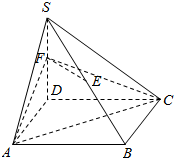 如图,四棱锥S-ABCD中,侧棱SD垂直于正方形ABCD所在的平面,E、F分别是SB、SD的中点,求证:
如图,四棱锥S-ABCD中,侧棱SD垂直于正方形ABCD所在的平面,E、F分别是SB、SD的中点,求证: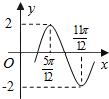 函数y=Asin(ωx+φ)(A>0,ω>0,|φ|≤$\frac{π}{2}$)的部分图象如图所示,则函数表达式为y=2sin(2x-$\frac{π}{3}$).
函数y=Asin(ωx+φ)(A>0,ω>0,|φ|≤$\frac{π}{2}$)的部分图象如图所示,则函数表达式为y=2sin(2x-$\frac{π}{3}$).