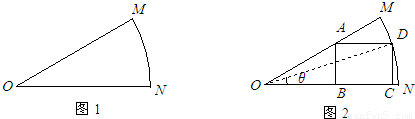题目内容
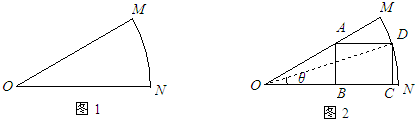 某车间为了制作某个零件,需从一块扇形的钢板余料(如图1)中按照图2的方式裁剪一块矩形钢板ABCD,其中顶点B、C在半径ON上,顶点A在半径OM上,顶点D在
某车间为了制作某个零件,需从一块扇形的钢板余料(如图1)中按照图2的方式裁剪一块矩形钢板ABCD,其中顶点B、C在半径ON上,顶点A在半径OM上,顶点D在 |
| NM |
| π |
| 6 |
(Ⅰ)用含θ的式子表示DC、OB的长;
(Ⅱ)试将S表示为θ的函数;
(Ⅲ)求S的最大值.
分析:(1)直接在三角形中利用三角函数可以表示DC、OB的长;
(2)S=BC×CD,由(1)可以求出相应函数;
(3)表达成θ的函数关系式,再利用导数方法研究函数的最大值,
(2)S=BC×CD,由(1)可以求出相应函数;
(3)表达成θ的函数关系式,再利用导数方法研究函数的最大值,
解答:解:(1)在△ODC中DC=sinθ,在△OAB中,tan
=
,从而OB=
sinθ;
(2)在△ODC中OC=cosθ,从而S=BC×CD=cosθsinθ -
sin2θ(0<θ<
)
(3)由S/=-sin2θ+cos2θ-2
sinθcosθ=0得tan2θ=
,由0<θ<
,得θ=
,易得θ=
时,S的最大值为1-
.
| π |
| 6 |
| AB |
| OB |
| 3 |
(2)在△ODC中OC=cosθ,从而S=BC×CD=cosθsinθ -
| 3 |
| π |
| 6 |
(3)由S/=-sin2θ+cos2θ-2
| 3 |
| ||
| 3 |
| π |
| 6 |
| π |
| 12 |
| π |
| 12 |
| ||
| 2 |
点评:解决实际问题的关键在于建立数学模型和目标函数,把“问题情境”译为数学语言,找出问题的主要关系,并把问题的主要关系抽象成数学问题,在数学领域寻找适当的方法解决,再返回到实际问题中加以说明.

练习册系列答案
相关题目
(本小题共12分)
某车间为了制作某个零件,需从一块扇形的钢板余料(如图1)中按照图2的方式裁剪一块矩形钢板![]() ,其中顶点
,其中顶点![]() 、
、![]() 在半径
在半径![]() 上,顶点
上,顶点![]() 在半径
在半径![]() 上,顶点
上,顶点![]() 在
在![]() 上,
上, ![]() ,
,![]() .设
.设![]() ,矩形
,矩形![]() 的面积为
的面积为![]() .
.
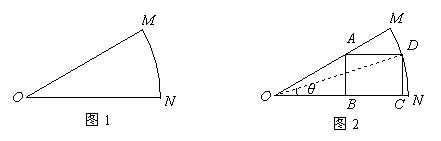 |
(Ⅰ)用含![]() 的式子表示
的式子表示![]() 、
、![]() 的长;
的长;
(Ⅱ)试将![]() 表示为
表示为![]() 的函数;
的函数;
(Ⅲ)求![]() 的最大值.
的最大值.

 上,
上, ,ON=OM=1.设∠DON=θ,矩形ABCD的面积为S.
,ON=OM=1.设∠DON=θ,矩形ABCD的面积为S.