题目内容
假设国家收购某种农产品的价格是1.2元/kg,其中征税标准为每100元征8元(叫做税率为8个百分点,即8%),计划可收购mkg.为了减轻农民负担,决定税率降低x个百分点,预计收购可增加2x个百分点.(1)写出税收y(元)与x的函数关系;
(2)要使此项税收在税率调节后不低于原计划的78%,确定x的取值范围.
【答案】分析:(1)根据题意先求出调节后税率及预计可收购量,税前总金额,最后根据税率公式即可求得税收y(元)与x的函数关系;
(2)根据原计划税收与税率调节后的税收之间的关系得出关于x的不等式,解此不等式即可得x的取值范围为0<x≤2.
解答:解:(1)由题知,调节后税率为(8-x)%,
预计可收购m(1+2x%)kg,总金额为1.2m(1+2x%)元
∴y=1.2m(1+2x%)(8-x)%=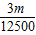 (400-42x-x2)(0<x≤8).
(400-42x-x2)(0<x≤8).
(2)∵原计划税收1.2m•8%元,
∴1.2m(1+2x%)(8-x)%≥1.2m•8%•78%,
得x2+42x-88≤0,-44≤x≤2,又∵0<x≤8,
∴x的取值范围为0<x≤2.
点评:本小题主要考查函数选择二次函数模型、二次函数性质的应用、税率等基础知识,属于基础题.
(2)根据原计划税收与税率调节后的税收之间的关系得出关于x的不等式,解此不等式即可得x的取值范围为0<x≤2.
解答:解:(1)由题知,调节后税率为(8-x)%,
预计可收购m(1+2x%)kg,总金额为1.2m(1+2x%)元
∴y=1.2m(1+2x%)(8-x)%=
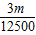 (400-42x-x2)(0<x≤8).
(400-42x-x2)(0<x≤8).(2)∵原计划税收1.2m•8%元,
∴1.2m(1+2x%)(8-x)%≥1.2m•8%•78%,
得x2+42x-88≤0,-44≤x≤2,又∵0<x≤8,
∴x的取值范围为0<x≤2.
点评:本小题主要考查函数选择二次函数模型、二次函数性质的应用、税率等基础知识,属于基础题.

练习册系列答案
 A加金题 系列答案
A加金题 系列答案 全优测试卷系列答案
全优测试卷系列答案
相关题目
 kg.为了减轻农民负担,决定税率降低
kg.为了减轻农民负担,决定税率降低 个百分点,预计收购可增加
个百分点,预计收购可增加 个百分点.
个百分点. (元)与
(元)与 kg.为了减轻农民负担,决定税率降低
kg.为了减轻农民负担,决定税率降低 个百分点,预计收购可增加
个百分点,预计收购可增加 个百分点.
个百分点. (元)与
(元)与