题目内容
已知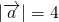 ,
, ,
,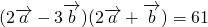
(1)求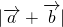 和
和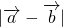 ;
;
(2)若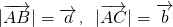 ,作△ABC,求△ABC的面积.
,作△ABC,求△ABC的面积.
解:(1)∵ =4,
=4, =4,由
=4,由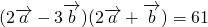 得:
得:
4 -4
-4 •
• -3
-3 =61,
=61,
∴ •
• =-
=- ,
,
∴ =
=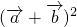 =
= +2
+2 •
• +
+ =
= ,
,
∴ =
=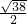 ,
,
同理可求得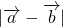 =
=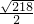 …6′
…6′
(2)cos∠BAC= =
=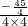 =-
=-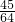 ,
,
∴sin∠BAC=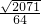 ,
,
∴S△ABC= |
| ||
|| |sin∠BAC=
|sin∠BAC= ×4×4×
×4×4×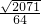 =
=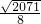 (12分)
(12分)
分析:(1)由题意可求得 •
• =-
=- ,从而可求得
,从而可求得 与
与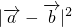 ,于是可得
,于是可得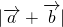 和
和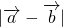 ;
;
(2)利用向量的夹角公式可求得cos∠BAC=-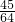 ,从而可求得sin∠BAC=
,从而可求得sin∠BAC=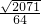 ,利用三角形的面积公式可求得S△ABC.
,利用三角形的面积公式可求得S△ABC.
点评:本题考查平面向量数量积的运算,着重考查向量的模的运算及向量的夹角,考查正弦定理的面积公式,属于中档题.
 =4,
=4, =4,由
=4,由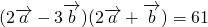 得:
得:4
 -4
-4 •
• -3
-3 =61,
=61,∴
 •
• =-
=- ,
,∴
 =
=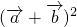 =
= +2
+2 •
• +
+ =
= ,
,∴
 =
=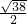 ,
,同理可求得
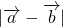 =
=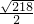 …6′
…6′(2)cos∠BAC=
 =
=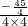 =-
=-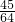 ,
,∴sin∠BAC=
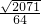 ,
,∴S△ABC=
 |
| ||
|| |sin∠BAC=
|sin∠BAC= ×4×4×
×4×4×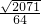 =
=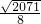 (12分)
(12分)分析:(1)由题意可求得
 •
• =-
=- ,从而可求得
,从而可求得 与
与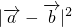 ,于是可得
,于是可得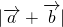 和
和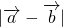 ;
;(2)利用向量的夹角公式可求得cos∠BAC=-
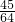 ,从而可求得sin∠BAC=
,从而可求得sin∠BAC=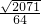 ,利用三角形的面积公式可求得S△ABC.
,利用三角形的面积公式可求得S△ABC.点评:本题考查平面向量数量积的运算,着重考查向量的模的运算及向量的夹角,考查正弦定理的面积公式,属于中档题.

练习册系列答案
相关题目
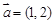 ,
,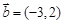 .
.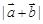 和
和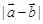 ;
;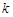 为何值时,
为何值时,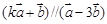 .
. ,
, .
. 和
和 ;
; 为何值时,
为何值时, .
.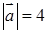 ,
,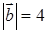 ,
,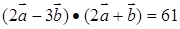
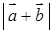 和
和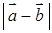 .
.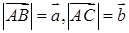 ,作
,作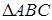 ,求
,求 ,
,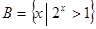

 和
和 ;
;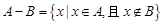 ,
, ”的部分用阴影涂黑;
”的部分用阴影涂黑;  和
和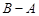 .
.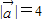 ,
, ,
,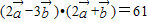
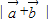 和
和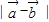 ;
;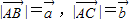 ,作△ABC,求△ABC的面积.
,作△ABC,求△ABC的面积.