题目内容
某次运动会甲、乙两名射击运动员成绩如下:
甲:9.4,8.7,7.5,8.4,10.1,10.5,10.7,7.2,7.8,10.8;
乙:9.1,8.7,7.1,9.8,9.7,8.5,10.1,9.2,10.1,9.1;
(1)用茎叶图表示甲,乙两个成绩;
(2)分别计算两个样本的平均数
和标准差s,并根据计算结果估计哪位运动员的成绩比较稳定.
甲:9.4,8.7,7.5,8.4,10.1,10.5,10.7,7.2,7.8,10.8;
乙:9.1,8.7,7.1,9.8,9.7,8.5,10.1,9.2,10.1,9.1;
(1)用茎叶图表示甲,乙两个成绩;
(2)分别计算两个样本的平均数
. | x |
分析:(1)用茎表示成绩的整数环数,叶表示小数点后的数字,画出茎叶图表示甲,乙两个人的成绩;
(2)利用平均值公式及标准差公式求出两个样本的平均数
和标准差s,根据标准差越大,波动越大,得到乙运动员的成绩比较稳定.
(2)利用平均值公式及标准差公式求出两个样本的平均数
. |
| x |
解答: 解:(1)如图所示,茎表示成绩的整数环数,叶表示小数点后的数字.(4分)
解:(1)如图所示,茎表示成绩的整数环数,叶表示小数点后的数字.(4分)
(2)解:
甲=
×(9.4+8.7+7.5+8.4+10.1+10.5+10.7+7.2+7.8+10.8)=9.11
S甲=
=1.3
乙=
×(9.1+8.7+7.1+9.8+9.7+8.5+10.1+9.2+10.1+9.1)=9.14
S乙=
=0.9
因为S甲>S乙,这说明了甲运动员的波动大于乙运动员的波动,
所以我们估计,乙运动员比较稳定. (12分)
 解:(1)如图所示,茎表示成绩的整数环数,叶表示小数点后的数字.(4分)
解:(1)如图所示,茎表示成绩的整数环数,叶表示小数点后的数字.(4分)(2)解:
. |
| x |
| 1 |
| 10 |
S甲=
|
. |
| x |
| 1 |
| 10 |
S乙=
|
因为S甲>S乙,这说明了甲运动员的波动大于乙运动员的波动,
所以我们估计,乙运动员比较稳定. (12分)
点评:本题考查茎叶图,考查根据样本数据的平均数、方差来确定数据的平均程度及样本数据稳定性情况,属于基础题.

练习册系列答案
相关题目
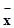 和标准差s,并根据计算结果估计哪位运动员的成绩比较稳定.
和标准差s,并根据计算结果估计哪位运动员的成绩比较稳定.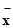 和标准差s,并根据计算结果估计哪位运动员的成绩比较稳定。
和标准差s,并根据计算结果估计哪位运动员的成绩比较稳定。