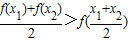题目内容
(类型A)已知函数f(x)=x2+| 2 |
| x |
(1)当a≤0时,
| f(x1)+f(x2) |
| 2 |
| x1+x2 |
| 2 |
(2)当a≤4时,|f′(x1)-f′(x2)|>|x1-x2|
(类型B)某旅行社在暑假期间推出如下旅游团组团办法:达到100人的团体,每人收费1000元.如果团体的人数超过100人,那么每超过1人,每人平均收费降低5元,但团体人数不能超过180人.如何组团,可使旅行社的收费最多?
分析:(类型A)(1)将x1,x2代入整理,整理出关于x1,x2的关系式,结合基本不等式使用条件,再由基本不等式可证.
(2)先对函数f(x)进行求导,将x1,x2代入整理变形,转化为证明对任意两个不相等的正数x1,x2,有 2+
-
>1恒成立,从而得证.
(类型B)设有x人参加旅行团,收费共y元,则有:y=1000x-5×(x-100)×x,(100≤x≤180),求出对称轴得到函数的最大值.
(2)先对函数f(x)进行求导,将x1,x2代入整理变形,转化为证明对任意两个不相等的正数x1,x2,有 2+
| 2(x1+x2) |
| x12x22 |
| a |
| x1x2 |
(类型B)设有x人参加旅行团,收费共y元,则有:y=1000x-5×(x-100)×x,(100≤x≤180),求出对称轴得到函数的最大值.
解答:解:(类型A)证明:(1)由 f(x)=x2+
+alnx
得
=
(x12+x22)+(
+
)+
(lnx1+lnx2)=
(x12+x22)+
+aln
f(
)=(
)2+
+aln
而
(x12+x22)>
[(x12+x22)+2x1x2]2=(
)2①
又(x1+x2)2=(x12+x22)+2x1x2>4x1x2
∴
>
②
∵
<
∴ln
<ln
∵a≤0
∴aln
>aln
③
由①、②、③得
(x12+x22)+
+aln
>(
)2+
+aln
即
>f(
).
(2):由 f(x)=x2+
+alnx,得 f′(x)=2x-
+
∴|f′(x1)-f′(x2)|=|(2x1-
+
)-(2x2-
+
)|=|x1-x2|•|2+
-
||f′(x1)-f′(x2)|>|x1-x2|?|2+
-
|>1
下面证明对任意两个不相等的正数x1,x2,有 2+
-
>1恒成立
即证 a<x1x2+
成立
∵x1x2+
>x1x2+
设 t=
,u(x)=t2+
(t>0),
则 u′(x)=2t-
,
令u′(x)=0得 t=
,列表如下:
 u(t)≥3
u(t)≥3
=
>4≥a
∴x1x2+
>a
∴对任意两个不相等的正数x1,x2,恒有|f'(x1)-f'(x2)|>|x1-x2|.
(类型B)设有x人参加旅行团,收费共y元,则有:
y=1000x-5×(x-100)×x,(100≤x≤180).
整理得:y=-5x2+1500x=-5(x-150)2+112500.
所以当x=150人时,旅行团的收费最多为112500元.
| 2 |
| x |
得
| f(x1)+f(x2) |
| 2 |
| 1 |
| 2 |
| 1 |
| x1 |
| 1 |
| x2 |
| a |
| 2 |
| 1 |
| 2 |
| x1+x2 |
| x1x2 |
| x1x2 |
| x1+x2 |
| 2 |
| x1+x2 |
| 2 |
| 4 |
| x1+x2 |
| x1+x2 |
| 2 |
而
| 1 |
| 2 |
| 1 |
| 4 |
| x1+x2 |
| 2 |
又(x1+x2)2=(x12+x22)+2x1x2>4x1x2
∴
| x1+x2 |
| x1x2 |
| 4 |
| x1+x2 |
∵
| x1x2 |
| x1+x2 |
| 2 |
∴ln
| x1x2 |
| x1+x2 |
| 2 |
∵a≤0
∴aln
| x1x2 |
| x1+x2 |
| 2 |
由①、②、③得
| 1 |
| 2 |
| x1+x2 |
| x1x2 |
| x1x2 |
| x1+x2 |
| 2 |
| 4 |
| x1+x2 |
| x1x2 |
即
| f(x1)+f(x2) |
| 2 |
| x1+x2 |
| 2 |
(2):由 f(x)=x2+
| 2 |
| x |
| 2 |
| x2 |
| a |
| x |
∴|f′(x1)-f′(x2)|=|(2x1-
| 2 |
| x12 |
| a |
| x1 |
| 2 |
| x22 |
| a |
| x2 |
| 2(x1+x2) |
| x12x22 |
| a |
| x1x2 |
| 2(x1+x2) |
| x12x22 |
| a |
| x1x2 |
下面证明对任意两个不相等的正数x1,x2,有 2+
| 2(x1+x2) |
| x12x22 |
| a |
| x1x2 |
即证 a<x1x2+
| 2(x1+x2) |
| x1x2 |
∵x1x2+
| 2(x1+x2) |
| x1x2 |
| 4 | ||
|
设 t=
| x1x2 |
| 4 |
| t |
则 u′(x)=2t-
| 4 |
| t2 |
令u′(x)=0得 t=
| 3 | 2 |
 u(t)≥3
u(t)≥3| 3 | 4 |
| 3 | 108 |
∴x1x2+
| 2(x1+x2) |
| x1x2 |
∴对任意两个不相等的正数x1,x2,恒有|f'(x1)-f'(x2)|>|x1-x2|.
(类型B)设有x人参加旅行团,收费共y元,则有:
y=1000x-5×(x-100)×x,(100≤x≤180).
整理得:y=-5x2+1500x=-5(x-150)2+112500.
所以当x=150人时,旅行团的收费最多为112500元.
点评:本小题主要考查导数的基本性质和应用,函数的性质和平均值不等式等知识及综合分析、推理论证的能力.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
 内是减函数,求a的取值范围.
内是减函数,求a的取值范围.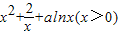 ,f(x)的导函数是f′(x),对任意两个不相等的正数x1,x2,证明:
,f(x)的导函数是f′(x),对任意两个不相等的正数x1,x2,证明: