题目内容
设an是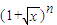 的展开式中x项的系数(n=2,3,4,…),则
的展开式中x项的系数(n=2,3,4,…),则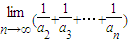 = .
= .
【答案】分析:由题意可知:an=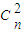 =
=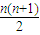 ,故
,故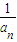 =
=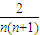 =2(
=2( -
-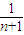 ),于是
),于是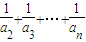 =2[(1-
=2[(1- )+(
)+( -
- )+…+(
)+…+(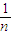 -
-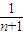 )],
)],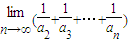 的值可求.
的值可求.
解答:解:∵an是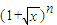 的展开式中x项的系数(n=2,3,4,…),
的展开式中x项的系数(n=2,3,4,…),
∴an=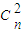 =
=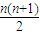 ,
,
∴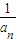 =
=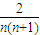 =2(
=2(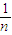 -
-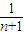 ),
),
∴是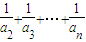 =2[(1-
=2[(1- )+(
)+( -
- )+…+(
)+…+(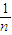 -
-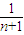 )]=2(1-
)]=2(1-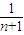 ),
),
∴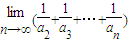 =
=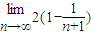 =2.
=2.
故答案为:2.
点评:本题考查二项式定理的应用及极限及其运算,着重考查裂项法求和及极限求值,属于中档题.
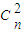 =
=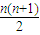 ,故
,故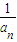 =
=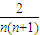 =2(
=2( -
-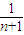 ),于是
),于是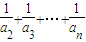 =2[(1-
=2[(1- )+(
)+( -
- )+…+(
)+…+(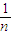 -
-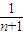 )],
)],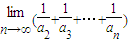 的值可求.
的值可求.解答:解:∵an是
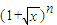 的展开式中x项的系数(n=2,3,4,…),
的展开式中x项的系数(n=2,3,4,…),∴an=
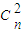 =
=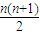 ,
,∴
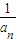 =
=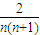 =2(
=2(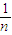 -
-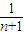 ),
),∴是
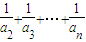 =2[(1-
=2[(1- )+(
)+( -
- )+…+(
)+…+(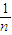 -
-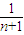 )]=2(1-
)]=2(1-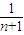 ),
),∴
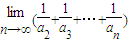 =
=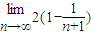 =2.
=2.故答案为:2.
点评:本题考查二项式定理的应用及极限及其运算,着重考查裂项法求和及极限求值,属于中档题.

练习册系列答案
 小学学习好帮手系列答案
小学学习好帮手系列答案 小学同步三练核心密卷系列答案
小学同步三练核心密卷系列答案
相关题目
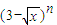 的展开式中x项的系数(n=2、3、4、…),则
的展开式中x项的系数(n=2、3、4、…),则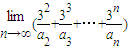 = .
= .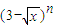 的展开式中x项的系数(n=2、3、4、…),则
的展开式中x项的系数(n=2、3、4、…),则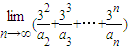 = .
= .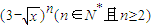 的展开式中x的系数,则
的展开式中x的系数,则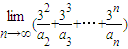 = .
= .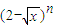 的展开式中x项的系数(n=2,3,4,…),则极限
的展开式中x项的系数(n=2,3,4,…),则极限 = .
= .