题目内容
若△ABC的三边长分别是3,7,9,则它的较大的锐角的平分线分三角形所成的两个三角形的面积之比是1:
3
3
.分析:不妨设AB=3,AC=7,BC=9,则由余弦定理及AB<AC可得C<B<90°即较大的锐角为B,由角平分线性质
=
可求
,由△ABD与△BCD的高相同可得
=
,从而可求
| AD |
| CD |
| AB |
| BC |
| AD |
| CD |
| S△ABD |
| S△CBD |
| AD |
| DC |
解答:解:不妨设AB=3,AC=7,BC=9
则由三角形的余弦定理可得,A>90°,B<90°,C<90°
∵AB<AC∴C<B<90° 则较大的锐角为B
由角平分线性质可得
=
=
由于△ABD与△BCD的高相同设为h
∴
=
=
=
故答案为:3.
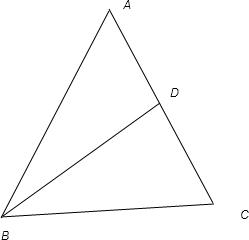
则由三角形的余弦定理可得,A>90°,B<90°,C<90°
∵AB<AC∴C<B<90° 则较大的锐角为B
由角平分线性质可得
| AB |
| BC |
| AD |
| CD |
| 1 |
| 3 |
由于△ABD与△BCD的高相同设为h
∴
| S△ABD |
| S△BCD |
| AD•h |
| CD•h |
| AD |
| CD |
| 1 |
| 3 |
故答案为:3.

点评:本题主要考查了三角形的余弦定理及大边对大角的应用,而角平分线性质的应用是解决本题的关键,从而把所要求的面积的比转化为线段的长度之比.

练习册系列答案
 口算题卡加应用题集训系列答案
口算题卡加应用题集训系列答案 综合自测系列答案
综合自测系列答案
相关题目

 成等差数列.
成等差数列. 与
与 的大小,并证明你的结论;
的大小,并证明你的结论;