题目内容
若1<x<3,a为何值时,x2-5x+3+a=0有两解、一解、无解?
【答案】分析:画出方程x2-5x+3=0对应函数y=-x2+5x-3(1<x<3)的图象,然后分析函数图象与直线y=a的交点的情况,即可得到答案.
解答: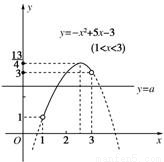 解:原方程化为:a=-x2+5x-3,①,
解:原方程化为:a=-x2+5x-3,①,
作出函数y=-x2+5x-3(1<x<3)的图象如图.
显然该图象与直线y=a的交点的横坐标是方程①的解,
由图可知:当3<a<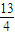 时,原方程有两解;
时,原方程有两解;
当1<a≤3或a=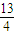 时,原方程有一解;
时,原方程有一解;
当a>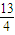 或a≤1时,原方程无解.
或a≤1时,原方程无解.
点评:本题考查的知识点是二次函数的性质,其中画出函数y=-x2+5x-3(1<x<3)的图象,是解答本题的关键.
解答:
 解:原方程化为:a=-x2+5x-3,①,
解:原方程化为:a=-x2+5x-3,①,作出函数y=-x2+5x-3(1<x<3)的图象如图.
显然该图象与直线y=a的交点的横坐标是方程①的解,
由图可知:当3<a<
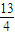 时,原方程有两解;
时,原方程有两解;当1<a≤3或a=
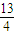 时,原方程有一解;
时,原方程有一解;当a>
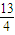 或a≤1时,原方程无解.
或a≤1时,原方程无解.点评:本题考查的知识点是二次函数的性质,其中画出函数y=-x2+5x-3(1<x<3)的图象,是解答本题的关键.

练习册系列答案
相关题目