题目内容
设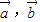 是任意的两个向量,λ∈R,给出下面四个结论:
是任意的两个向量,λ∈R,给出下面四个结论:①若
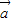 与
与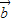 共线,则
共线,则 =λ
=λ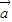 ;
;②若
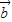 =-λ
=-λ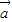 ,则
,则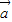 与
与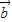 共线;③若
共线;③若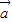 =λ
=λ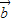 ,则
,则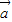 与
与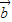 共线;
共线;④当
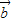 ≠0时,
≠0时,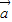 与
与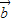 共线的充要条件是有且只有一个实数λ=λ1,使得
共线的充要条件是有且只有一个实数λ=λ1,使得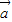 =λ1
=λ1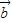 .
.其中正确的结论有( )
A.①②
B.①③
C.①③④
D.②③④
【答案】分析:通过举反例判断出①错;据数乘运算的定义判断出②③对;据两向量共线的充要条件判断出④对.
解答:解:对于①当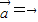 时,满足两向量共线但不存在λ使
时,满足两向量共线但不存在λ使 故①错
故①错
对于②③根据数乘运算的定义知正确;
对于④由两向量共线的充要条件得到对.
故②③④正确.
故选D
点评:题目考查两向量共线的充要条件: ??
??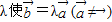
此定理应把握好两点:①与λ相乘的向量为非零向量,②λ存在且唯一.
解答:解:对于①当
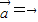 时,满足两向量共线但不存在λ使
时,满足两向量共线但不存在λ使 故①错
故①错对于②③根据数乘运算的定义知正确;
对于④由两向量共线的充要条件得到对.
故②③④正确.
故选D
点评:题目考查两向量共线的充要条件:
 ??
??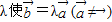
此定理应把握好两点:①与λ相乘的向量为非零向量,②λ存在且唯一.

练习册系列答案
相关题目
 是任意的两个向量,λ∈R,给出下面四个结论:
是任意的两个向量,λ∈R,给出下面四个结论: 与
与 共线,则
共线,则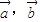 是任意的两个向量,λ∈R,给出下面四个结论:
是任意的两个向量,λ∈R,给出下面四个结论: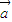 与
与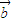 共线,则
共线,则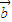 =λ
=λ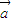 ;
;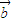 =-λ
=-λ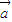 ,则
,则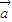 与
与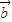 共线;③若
共线;③若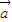 =λ
=λ ,则
,则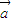 与
与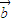 共线;
共线;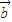 ≠0时,
≠0时,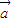 与
与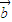 共线的充要条件是有且只有一个实数λ=λ1,使得
共线的充要条件是有且只有一个实数λ=λ1,使得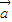 =λ1
=λ1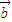 .
.