题目内容
现有下面四个命题:①曲线y=-x2+2x+4在点(1,5)处的切线的倾斜角为45°;
②已知直线l,m,平面α,β,若l⊥α,m?β,l⊥m,则α∥β;
③设函数f(x)=Asin(ωx+φ),(A>0,ω>0),若f(1)=0,
则f(x+1)一定是奇函数;
④如果点P到点A(
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |
其中正确命题的序号是
分析:①曲线y=-x2+2x+4在点(1,5)处的切线的倾斜角为45°,求出切点处的导数值,进行验证;
②已知直线l,m,平面α,β,若l⊥α,m?β,l⊥m,则α∥β,由面面位置关系进行判断;
③设函数f(x)=Asin(ωx+φ),(A>0,ω>0),若f(1)=0,则f(x+1)一定是奇函数,求出两参数ω,φ的关系,整理解析式,观察既得;
④如果点P到点A(
,0),B(
,2)及直线x=-
的距离相等,那么满足条件的点P有且只有1个,由两直线的交点个数研究即可.
②已知直线l,m,平面α,β,若l⊥α,m?β,l⊥m,则α∥β,由面面位置关系进行判断;
③设函数f(x)=Asin(ωx+φ),(A>0,ω>0),若f(1)=0,则f(x+1)一定是奇函数,求出两参数ω,φ的关系,整理解析式,观察既得;
④如果点P到点A(
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |
解答:解:①曲线y=-x2+2x+4在点(1,5)处的切线的倾斜角为45°.是错误命题,因为y′=-2x+2,在点(1,5)处的导数值为0,故倾斜角不是45°;
②已知直线l,m,平面α,β,若l⊥α,m?β,l⊥m,则α∥β是错误命题,在题设中的条件下,两平面可以是相交的;
③设函数f(x)=Asin(ωx+φ),(A>0,ω>0),若f(1)=0,则f(x+1)一定是奇函数,是正确命题,由f(1)=0,得出ω+φ=0,函数解析式可变为f(x)=Asinω(x-1),左移一个单位可得到f(x)=Asinωx是一个奇函数;
④如果点P到点A(
,0),B(
,2)及直线x=-
的距离相等,那么满足条件的点P有且只有1个,是正确命题,作出两点的垂直平分线y=1,与直线x=-
相交,故满足条件的点只有一个.
综上③④是正确命题
故答案为③④
②已知直线l,m,平面α,β,若l⊥α,m?β,l⊥m,则α∥β是错误命题,在题设中的条件下,两平面可以是相交的;
③设函数f(x)=Asin(ωx+φ),(A>0,ω>0),若f(1)=0,则f(x+1)一定是奇函数,是正确命题,由f(1)=0,得出ω+φ=0,函数解析式可变为f(x)=Asinω(x-1),左移一个单位可得到f(x)=Asinωx是一个奇函数;
④如果点P到点A(
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |
综上③④是正确命题
故答案为③④
点评:本题考查奇函数,函数图象的变换,导数的几何意义等内容,解答本题的关键是对本题中命题所涉及到的相关知识点都比较熟悉,方能避免误判.本题是考查双基的题.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
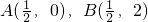 及直线
及直线 的距离相等,那么满足条件的点P有且只有1个.
的距离相等,那么满足条件的点P有且只有1个.