题目内容
设函数f(x)=cos2x+asin2x,若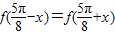 ,那么a等于 .
,那么a等于 .
【答案】分析:有条件可得函数f(x)关于直线 x=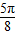 对称,故有f(
对称,故有f(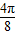 )=f(
)=f(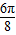 ),解方程求得a的值.
),解方程求得a的值.
解答:解:∵函数f(x)满足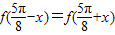 ,则函数f(x)关于直线 x=
,则函数f(x)关于直线 x=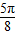 对称,
对称,
∴f(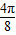 )=f(
)=f(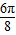 ),∴cosπ+asinπ=cos
),∴cosπ+asinπ=cos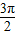 +asin
+asin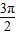 ,即-1=0-a,
,即-1=0-a,
∴a=1,
故答案为1.
点评:本题考查函数的对称性,判断函数f(x)关于直线 x=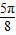 对称,是解题的关键.
对称,是解题的关键.
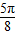 对称,故有f(
对称,故有f(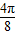 )=f(
)=f(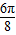 ),解方程求得a的值.
),解方程求得a的值.解答:解:∵函数f(x)满足
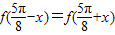 ,则函数f(x)关于直线 x=
,则函数f(x)关于直线 x=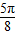 对称,
对称,∴f(
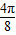 )=f(
)=f(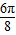 ),∴cosπ+asinπ=cos
),∴cosπ+asinπ=cos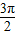 +asin
+asin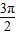 ,即-1=0-a,
,即-1=0-a,∴a=1,
故答案为1.
点评:本题考查函数的对称性,判断函数f(x)关于直线 x=
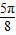 对称,是解题的关键.
对称,是解题的关键. 
练习册系列答案
 鸿图图书寒假作业假期作业吉林大学出版社系列答案
鸿图图书寒假作业假期作业吉林大学出版社系列答案
相关题目