题目内容
已知向量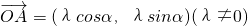 ,
,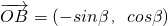 ,其中O为坐标原点,若|
,其中O为坐标原点,若| |≥2|
|≥2| |对任意的实数α,β都成立,则实数λ的取值范围是________.
|对任意的实数α,β都成立,则实数λ的取值范围是________.
(-∞,-3]∪[3,+∞)
分析:先求出A、B两点的坐标,再求 的坐标表示,代入已知的不等式进行化简,最后利用三角函数的范围求出λ的范围.
的坐标表示,代入已知的不等式进行化简,最后利用三角函数的范围求出λ的范围.
解答:由题意知,A(λcosα,λsinα),B(-sinβ,cosβ),
∴ =(λcosα+sinβ,λsinα-cosβ),∵|
=(λcosα+sinβ,λsinα-cosβ),∵| |≥2|
|≥2| |恒成立,
|恒成立,
∴(λcosα+sinβ)(λcosα+sinβ)+(λsinα-cosβ)(λsinα-cosβ)≥4,
λ2+1+2λcosαsinβ-2λsinαcosβ≥4,
λ2+2λsin(β-α)-3≥0,
∵|sin(β-α)|≤1,∴λ2+2λ-3≥0且λ2-2λ-3≥0,
解得,λ≤-3或λ≥1 且λ≤-1或λ≥3
∴λ≤-3或λ≥3.
故答案为:(-∞,-3]∪[3,+∞).
点评:本题考查了向量的坐标运算,包括求向量以及向量的长度,在化简中用到了两角和差的正弦公式及正弦值的范围,来解决恒成立问题.
分析:先求出A、B两点的坐标,再求
 的坐标表示,代入已知的不等式进行化简,最后利用三角函数的范围求出λ的范围.
的坐标表示,代入已知的不等式进行化简,最后利用三角函数的范围求出λ的范围.解答:由题意知,A(λcosα,λsinα),B(-sinβ,cosβ),
∴
 =(λcosα+sinβ,λsinα-cosβ),∵|
=(λcosα+sinβ,λsinα-cosβ),∵| |≥2|
|≥2| |恒成立,
|恒成立,∴(λcosα+sinβ)(λcosα+sinβ)+(λsinα-cosβ)(λsinα-cosβ)≥4,
λ2+1+2λcosαsinβ-2λsinαcosβ≥4,
λ2+2λsin(β-α)-3≥0,
∵|sin(β-α)|≤1,∴λ2+2λ-3≥0且λ2-2λ-3≥0,
解得,λ≤-3或λ≥1 且λ≤-1或λ≥3
∴λ≤-3或λ≥3.
故答案为:(-∞,-3]∪[3,+∞).
点评:本题考查了向量的坐标运算,包括求向量以及向量的长度,在化简中用到了两角和差的正弦公式及正弦值的范围,来解决恒成立问题.

练习册系列答案
相关题目
 =
= ,
, =
=
 =
= ,其中O为坐标原点,且0<α<
,其中O为坐标原点,且0<α< <β<π
<β<π ,求β-α的值;
,求β-α的值; =2,
=2, ,求△OAB的面积S.
,求△OAB的面积S.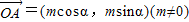 ,
,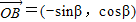 .其中O为坐标原点.
.其中O为坐标原点.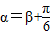 且m>0,求向量
且m>0,求向量 与
与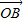 的夹角;
的夹角;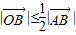 对任意实数α、β都成立,求实数m的取值范围.
对任意实数α、β都成立,求实数m的取值范围. ,
, ,其中O为坐标原点,若|
,其中O为坐标原点,若| |≥2|
|≥2| |对任意的实数α,β都成立,则实数λ的取值范围是 .
|对任意的实数α,β都成立,则实数λ的取值范围是 .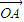 =
= ,
,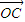 =
=
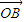 =
=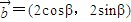 ,其中O为坐标原点,且0<α<
,其中O为坐标原点,且0<α<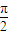 <β<π
<β<π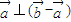 ,求β-α的值;
,求β-α的值;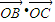 =2,
=2,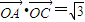 ,求△OAB的面积S.
,求△OAB的面积S. ,
,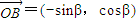 .其中O为坐标原点.
.其中O为坐标原点. 且m>0,求向量
且m>0,求向量 与
与 的夹角;
的夹角; 对任意实数α、β都成立,求实数m的取值范围.
对任意实数α、β都成立,求实数m的取值范围.