题目内容
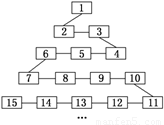
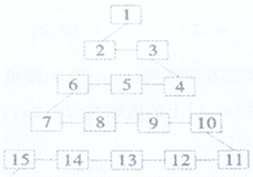 如图是网络工作者经常用来解释网络运作的蛇形模型:数字1出现在第1行;数字2,3出现在第2行;数字6,5,4(从左至右)出现在第3行;数字7,8,9,10出现在第4行;以此类推,则
如图是网络工作者经常用来解释网络运作的蛇形模型:数字1出现在第1行;数字2,3出现在第2行;数字6,5,4(从左至右)出现在第3行;数字7,8,9,10出现在第4行;以此类推,则(1)按网络运作顺序第n行第一个数字(如第2行第1个数字为2,第3行第1个数字为4,…)是
| n2-n+2 |
| 2 |
| n2-n+2 |
| 2 |
(2)第63行从左至右的第4个数应是
2013
2013
.分析:(1)前n行的数字个数之和刚好等于本行的最大数字,并且奇数行,从大到小排列;偶数行,从小到大排列,所以利用等差数列的求和公式,即可求得结论;
(2)第63行的数字从左至右是由大到小出现的,64行的数字从左至右是由小到大出现的,且第一个数字为2017,即可得到结论.
(2)第63行的数字从左至右是由大到小出现的,64行的数字从左至右是由小到大出现的,且第一个数字为2017,即可得到结论.
解答:解:(1)由题意,前(n-1)行一共已出现了1+2+3+…+(n-1)=
个数字,
∴按网络运作顺序第n行第一个数字是
+1=
;
(2)第63行的数字从左至右是由大到小出现的,64行的数字从左至右是由小到大出现的,且第一个数字为2017
∴第63行的数字从左至右依次为2016,2015,2014,2013,…,1954,
∴第63行从左至右的第4个数应是2013
故答案为:
,2013.
| n(n-1) |
| 2 |
∴按网络运作顺序第n行第一个数字是
| n(n-1) |
| 2 |
| n2-n+2 |
| 2 |
(2)第63行的数字从左至右是由大到小出现的,64行的数字从左至右是由小到大出现的,且第一个数字为2017
∴第63行的数字从左至右依次为2016,2015,2014,2013,…,1954,
∴第63行从左至右的第4个数应是2013
故答案为:
| n2-n+2 |
| 2 |
点评:本题考查合情推理,考查等差数列求和公式的运用,考查学生的计算能力,属于基础题.

练习册系列答案
相关题目
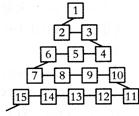 如图是网络工作者经常用来解释网络运作的蛇形模型:数字1出现在第1行;数字2,3出现在第2行,数字6,5,4(从左至右)出现在第3行;数字7,8,9,10出现在第4行;依此类推,则第63行从左至右算第8个数字为( )
如图是网络工作者经常用来解释网络运作的蛇形模型:数字1出现在第1行;数字2,3出现在第2行,数字6,5,4(从左至右)出现在第3行;数字7,8,9,10出现在第4行;依此类推,则第63行从左至右算第8个数字为( ) 如图是网络工作者经常用来解释网络动作的蛇形模型:数字1出现在第1行;数字2,3出现在第2行;数字6,5,4(从左至右)出现在第3行;数字7,8,9,10出现在第4行;依此类推,则第23行从左至右算第4个数字为.( )
如图是网络工作者经常用来解释网络动作的蛇形模型:数字1出现在第1行;数字2,3出现在第2行;数字6,5,4(从左至右)出现在第3行;数字7,8,9,10出现在第4行;依此类推,则第23行从左至右算第4个数字为.( ) 如图是网络工作者经常用来解释网络运作的蛇形模型:数字1出现在第1行;数字2,3出现在第2行;数字6,5,4(从左至右)出现在第3行;数字7,8,9,10出现在第4行;依此类推,则第63行从左至右的第5个数应是
如图是网络工作者经常用来解释网络运作的蛇形模型:数字1出现在第1行;数字2,3出现在第2行;数字6,5,4(从左至右)出现在第3行;数字7,8,9,10出现在第4行;依此类推,则第63行从左至右的第5个数应是