题目内容
已知y=Asin(ωx+φ),(A>0,ω>0)的图象过点P(
,0),图象上与点P最近的一个顶点是Q(
,5).
(1)求函数的解析式;并用“五点法”画简图;
(2)指出函数的增区间;
(3)求使y≤0的x的取值范围.
| π |
| 12 |
| π |
| 3 |
(1)求函数的解析式;并用“五点法”画简图;
(2)指出函数的增区间;
(3)求使y≤0的x的取值范围.
分析:(1)由已知中函数的图象过两个点,可以求出A,根据两点之间的横坐标之差为四分之一个周期,可以求出函数的周期,进而得到ω的值,将 (
,5)点代入求出φ值后,即可得到函数解析式.画出函数的图象.
(2)通过正弦函数的单调增区间直接函数的增区间;
(3)根据正弦函数的小于0的范围,得到关于x的不等式,得到函数值小于0时的自变量的取值.
| π |
| 3 |
(2)通过正弦函数的单调增区间直接函数的增区间;
(3)根据正弦函数的小于0的范围,得到关于x的不等式,得到函数值小于0时的自变量的取值.
解答:解:(1)由已知点函数y=Asin(ωx+φ)的图象过点 P(
,0),
图象中与点P最近的最高点是 (
,5),
∴A=5,
=
-
=
∴T=π
∴ω=
=2
∴y=5sin(2x+φ)
将 (
,5)代入解析式得
5=5sin(
+φ)
∴
+φ=2kπ+
,k∈z
∴φ=-
+2kπ,k∈Z
∵|φ|<π
令k=0,则有φ=-
∴y=5sin(2x-
),
列表如下:
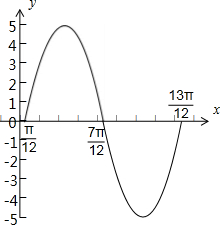
(2)由2kπ-
≤2x-
≤2kπ+
.
得增区间为[kπ-
,kπ+
].k∈Z.
函数的增区间:[kπ-
,kπ+
].k∈Z.
(3)∵y=sinx的满足y≤0的x的取值范围是[2kπ-π,2kπ],k∈z
∴y=5sin(2x-
)≤0时,有2x-
∈[2kπ-π,2kπ],
∴x∈[kπ-
π,kπ+
π](k∈Z).
| π |
| 12 |
图象中与点P最近的最高点是 (
| π |
| 3 |
∴A=5,
| T |
| 4 |
| π |
| 3 |
| π |
| 12 |
| π |
| 4 |
∴T=π
∴ω=
| 2π |
| T |
∴y=5sin(2x+φ)
将 (
| π |
| 3 |
5=5sin(
| 2π |
| 3 |
∴
| 2π |
| 3 |
| π |
| 2 |
∴φ=-
| π |
| 6 |
∵|φ|<π
令k=0,则有φ=-
| π |
| 6 |
∴y=5sin(2x-
| π |
| 6 |
列表如下:
| x |
|
|
|
|
| ||||||||||
2x-
|
0 |
|
π |
|
2π | ||||||||||
sin(2x-
|
0 | 1 | 0 | -1 | 0 | ||||||||||
| y | 0 | 5 | 0 | -5 | 0 |

(2)由2kπ-
| π |
| 2 |
| π |
| 6 |
| π |
| 2 |
得增区间为[kπ-
| π |
| 6 |
| π |
| 3 |
函数的增区间:[kπ-
| π |
| 6 |
| π |
| 3 |
(3)∵y=sinx的满足y≤0的x的取值范围是[2kπ-π,2kπ],k∈z
∴y=5sin(2x-
| π |
| 6 |
| π |
| 6 |
∴x∈[kπ-
| 5 |
| 12 |
| 1 |
| 12 |
点评:本题考查由y=Asin(ωx+φ)的部分图象确定其解析式,正弦函数的定义域和值域,本题解题的关键是根据已知条件求出A,ω,φ值,得到函数的解析式,这样才可以求解自变量的范围,本题是一个中档题目.

练习册系列答案
相关题目
 已知y=Asin(ωx+?)的最大值为1,在区间[
已知y=Asin(ωx+?)的最大值为1,在区间[| π |
| 6 |
| 2π |
| 3 |
A、(0,
| ||||
B、(0,
| ||||
C、(0,
| ||||
| D、以上都不是 |