题目内容
已知向量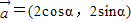 ,
,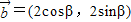 ,且直线2xcosα-2ysinα+1=0与圆(x-cosβ)2+(y+sinβ)2=1相切,则向量
,且直线2xcosα-2ysinα+1=0与圆(x-cosβ)2+(y+sinβ)2=1相切,则向量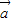 与
与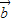 的夹角为 .
的夹角为 .
【答案】分析:利用直线与圆相切的充要条件:圆心到直线的距离等于圆的半径,再利用向量夹角的余弦等于两向量的数量积除以它们的模
解答:解:∵直线2xcosα-2ysinα+1=0与圆(x-cosβ)2+(y+sinβ)2=1相切,
∴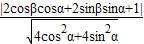 =1
=1
解得
向量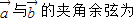
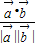 =
=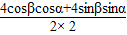 =
=
故两向量的夹角为60°
故答案为60°
点评:本题考查直线与圆相切的充要条件及向量数量积的应用:求夹角.
解答:解:∵直线2xcosα-2ysinα+1=0与圆(x-cosβ)2+(y+sinβ)2=1相切,
∴
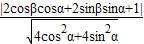 =1
=1解得

向量
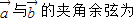
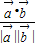 =
=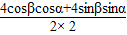 =
=
故两向量的夹角为60°
故答案为60°
点评:本题考查直线与圆相切的充要条件及向量数量积的应用:求夹角.

练习册系列答案
 通城学典默写能手系列答案
通城学典默写能手系列答案 金牌教辅培优优选卷期末冲刺100分系列答案
金牌教辅培优优选卷期末冲刺100分系列答案
相关题目
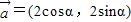 ,
,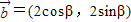 ,且直线2xcosα-2ysinα+1=0与圆(x-cosβ)2+(y+sinβ)2=1相切,则向量
,且直线2xcosα-2ysinα+1=0与圆(x-cosβ)2+(y+sinβ)2=1相切,则向量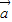 与
与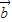 的夹角为 .
的夹角为 .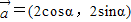 ,
,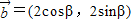 ,且直线2xcosα-2ysinα+1=0与圆(x-cosβ)2+(y+sinβ)2=1相切,则向量
,且直线2xcosα-2ysinα+1=0与圆(x-cosβ)2+(y+sinβ)2=1相切,则向量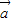 与
与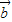 的夹角为 .
的夹角为 .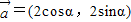 ,
,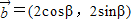 ,且直线2xcosα-2ysinα+1=0与圆(x-cosβ)2+(y+sinβ)2=1相切,则向量
,且直线2xcosα-2ysinα+1=0与圆(x-cosβ)2+(y+sinβ)2=1相切,则向量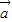 与
与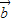 的夹角为 .
的夹角为 .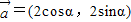 ,
,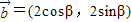 ,且直线2xcosα-2ysinα+1=0与圆(x-cosβ)2+(y+sinβ)2=1相切,则向量
,且直线2xcosα-2ysinα+1=0与圆(x-cosβ)2+(y+sinβ)2=1相切,则向量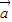 与
与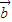 的夹角为 .
的夹角为 . ,
, ,且直线2xcosα-2ysinα+1=0与圆(x-cosβ)2+(y+sinβ)2=1相切,则向量
,且直线2xcosα-2ysinα+1=0与圆(x-cosβ)2+(y+sinβ)2=1相切,则向量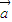 与
与 的夹角为 .
的夹角为 .