题目内容
设圆台的上下底面半径分别为10和15,母线长为30,则它的侧面展开图扇环中,两个相对顶点间的距离是
- A.60
- B.90
- C.
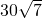
- D.
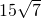
C
分析:利用圆台与圆锥的关系,及圆锥轴截面的对称性,可求得该圆锥的母线长,将圆台的问题转化为圆锥的问题,然后利用余弦定理可解得两个相对顶点间的距离.
解答: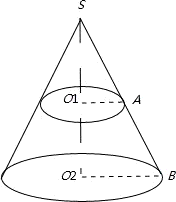 解:设SA=x,O1A=10,O2B=15,
解:设SA=x,O1A=10,O2B=15,
∵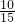 =
= ∴x=60,
∴x=60,
设圆台的侧面展开图扇环为AA'B'B,
∴∠A'SA=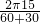 =
= ,
,
∴在△SAB'中,由余弦定理可得:AB'2=602+902-2×60×90×cos =900×7,
=900×7,
∴AB'=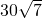 ,
,
故选C.
点评:本题看出来圆台,圆锥的相关问题,以及利用余弦定理其解三角形,是个基础题.
分析:利用圆台与圆锥的关系,及圆锥轴截面的对称性,可求得该圆锥的母线长,将圆台的问题转化为圆锥的问题,然后利用余弦定理可解得两个相对顶点间的距离.
解答:
 解:设SA=x,O1A=10,O2B=15,
解:设SA=x,O1A=10,O2B=15,∵
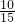 =
= ∴x=60,
∴x=60,设圆台的侧面展开图扇环为AA'B'B,
∴∠A'SA=
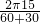 =
= ,
,∴在△SAB'中,由余弦定理可得:AB'2=602+902-2×60×90×cos
 =900×7,
=900×7,∴AB'=
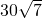 ,
,故选C.
点评:本题看出来圆台,圆锥的相关问题,以及利用余弦定理其解三角形,是个基础题.

练习册系列答案
相关题目
设圆台的上下底面半径分别为10和15,母线长为30,则它的侧面展开图扇环中,两个相对顶点间的距离是( )
| A、60 | ||
| B、90 | ||
C、30
| ||
D、15
|