题目内容
已知动点M到点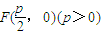 的距离比它到y轴的距离多
的距离比它到y轴的距离多 .
.(I)求动点M的轨迹方程;
(II)设动点M的轨迹为C,过点F的直线l与曲线C交于A、B两点,若y轴正半轴上存在点P使得△PAB是以P为直角顶点的等腰直角三角形,求直线l的方程.
【答案】分析:(I)由题知,点M到点F的距离与它到直线x=- 的距离相等,根据抛物线的定义能求出点M的轨迹方程.
的距离相等,根据抛物线的定义能求出点M的轨迹方程.
(II)设A(x1,y1),B(x2,y2),AB的中点D(x,y),直线l: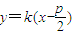 ,联立
,联立 ,得
,得 ,由此入手,能求出直线l的方程.
,由此入手,能求出直线l的方程.
解答:解:(I)由题知,点M到点F的距离与它到直线x=- 的距离相等,
的距离相等,
根据抛物线的定义,知点M的轨迹方程为y2=2px.
(II)设A(x1,y1),B(x2,y2),AB的中点D(x,y),直线l: ,
,
联立 ,得
,得 ,
,
则 ,
, ,
,
∴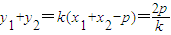 ,
,
 =-p2,
=-p2,
∴ ,由题知
,由题知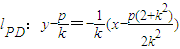 ,
,
令x=0得,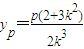 ,
,
又PA⊥PB,
∴ ,
,
化简,得yp2-(y1+y2)yp+y1y2+x1x2=0,
即3k6+3k4-4k2-4=0,
(3k4-4)(k2+1)=0,
解得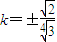 (舍负),
(舍负),
∴直线l的方程: .
.
点评:本题主要考查抛物线标准方程,简单几何性质,直线与抛物线的位置关系,抛物线的简单性质等基础知识.考查运算求解能力,推理论证能力;考查函数与方程思想,化归与转化思想.
 的距离相等,根据抛物线的定义能求出点M的轨迹方程.
的距离相等,根据抛物线的定义能求出点M的轨迹方程.(II)设A(x1,y1),B(x2,y2),AB的中点D(x,y),直线l:
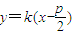 ,联立
,联立 ,得
,得 ,由此入手,能求出直线l的方程.
,由此入手,能求出直线l的方程.解答:解:(I)由题知,点M到点F的距离与它到直线x=-
 的距离相等,
的距离相等,根据抛物线的定义,知点M的轨迹方程为y2=2px.
(II)设A(x1,y1),B(x2,y2),AB的中点D(x,y),直线l:
 ,
,联立
 ,得
,得 ,
,则
 ,
, ,
,∴
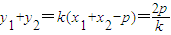 ,
, =-p2,
=-p2,∴
 ,由题知
,由题知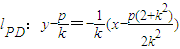 ,
,令x=0得,
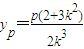 ,
,又PA⊥PB,
∴
 ,
,化简,得yp2-(y1+y2)yp+y1y2+x1x2=0,
即3k6+3k4-4k2-4=0,
(3k4-4)(k2+1)=0,
解得
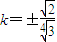 (舍负),
(舍负),∴直线l的方程:
 .
.点评:本题主要考查抛物线标准方程,简单几何性质,直线与抛物线的位置关系,抛物线的简单性质等基础知识.考查运算求解能力,推理论证能力;考查函数与方程思想,化归与转化思想.

练习册系列答案
相关题目
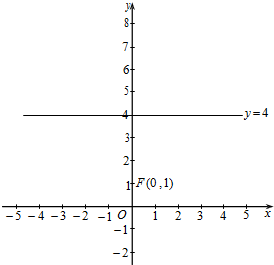 (2013•深圳二模)已知动点 M 到点 F(0,1)的距离与到直线 y=4 的距离之和为 5.
(2013•深圳二模)已知动点 M 到点 F(0,1)的距离与到直线 y=4 的距离之和为 5.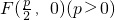 的距离比它到y轴的距离多
的距离比它到y轴的距离多 .
.