题目内容
函数 的部分图象如图所示,设P是图象的最高点,A,B是图象与x轴的交点,则tan∠APB等于
的部分图象如图所示,设P是图象的最高点,A,B是图象与x轴的交点,则tan∠APB等于
| A.10 | B.8 |
C. | D. |
B
解析试题分析:函数y=sin(πx+φ),∴T=2,最大值为1,
过p作PD⊥x轴于D,则AD是四分之一个周期,有AD= ,DB=
,DB=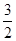 ,DP=1,
,DP=1,
在直角三角形中有tan∠APD= 与tan∠BPD=
与tan∠BPD=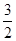 ,
,
所以tan∠APB=tan(∠APD+∠BPD)= =8,故选B.
=8,故选B.
考点:本题主要考查正弦型函数的图象和性质,两角和与差的正切公式
点评:中档题,结合图形分析,并通过做辅助线,在直角三角形中确定焦点正切,是解决问题的关键。

练习册系列答案
相关题目
 的最大值为
的最大值为
A. | B. | C. | D. |
在(0,2π)内,使sinx>cosx成立的x的取值范围是( )
A.( , , )∪(π, )∪(π, ) ) | B.( ,π) ,π) |
C.( , , ) ) | D.( ,π)∪( ,π)∪( , , ) ) |
要得到 的图象,只需将
的图象,只需将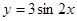 的图象( )
的图象( )
A.左移 个单位 个单位 | B.右移 个单位. 个单位. | C.左移 个单位 个单位 | D.右移 个单位 个单位 |
已知函数 ,若
,若 ,则
,则 与
与 的大小关系是( )
的大小关系是( )
A. > > | B. < < |
C. = = | D.大小与a、 有关 有关 |
要得到函数 的图象,只需将函数
的图象,只需将函数 的图象( )
的图象( )
A.右移 个单位 个单位 | B.右移 个单位 个单位 |
C.左移 个单位 个单位 | D.左移 个单位 个单位 |
 最小值是 ( )
最小值是 ( )
| A.-1 | B. | C. | D.1 |
已知函数 ,其中
,其中 为实数,若
为实数,若 对
对 恒成立,且
恒成立,且 ,则
,则 的单调递增区间是( ).
的单调递增区间是( ).
A. | B. |
C. | D. |
 的部分图象大致是( )
的部分图象大致是( )