题目内容
两座灯塔A和B与海洋观察站C的距离都等于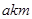 ,灯塔A在观察站C的北偏东20°.灯塔B在观察站C的南偏东40°,则灯塔A与灯塔B的距离为( )
,灯塔A在观察站C的北偏东20°.灯塔B在观察站C的南偏东40°,则灯塔A与灯塔B的距离为( )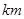 .
.
A.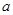 | B.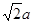 | C.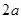 | D.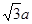 |
D
解析试题分析:作出图如图所示,由图知,∠ACB=120o,AC=BC=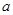 ,由余弦定理得
,由余弦定理得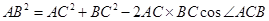 =
=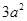 ,所以AB=
,所以AB= ,故选D.
,故选D.
考点:正余弦定理应用;余弦定理

练习册系列答案
 全优点练单元计划系列答案
全优点练单元计划系列答案
相关题目
在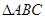 中,
中, , 则B的值为( )
, 则B的值为( )
A.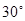 | B.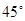 | C.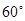 | D.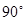 |
钝角三角形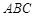 的面积是
的面积是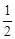 ,
,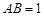 ,
,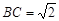 ,则
,则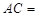 ( )
( )
| A.5 | B.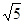 | C.2 | D.1 |
△ 各角的对应边分别为
各角的对应边分别为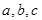 ,满足
,满足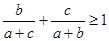 ,则角
,则角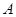 的范围是( )
的范围是( )
A.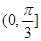 | B.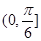 | C.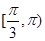 | D.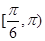 |
在 中,角
中,角 所对的边分别为
所对的边分别为 ,那么下列给出的各组条件能确定三角形有两解的是( )
,那么下列给出的各组条件能确定三角形有两解的是( )
A.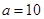 , ,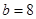 , ,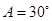 | B.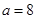 , ,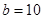 , ,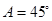 |
C.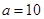 , ,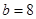 , ,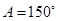 | D.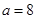 , ,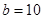 , ,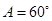 |
在三角形ABC中, ,则三角形△ABC为( ).
,则三角形△ABC为( ).
| A.等腰直角三角形 | B.等腰三角形 |
| C.等边三角形 | D.直角三角形 |
已知 中,
中, 分别为
分别为 的对边,
的对边, ,则
,则 等于( )
等于( )
A. | B. 或 或 | C. | D. 或 或 |
在△ABC中,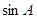 :
: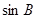 :
: =2:3:x,且△ABC为锐角三角形,则x的取值范围是( )
=2:3:x,且△ABC为锐角三角形,则x的取值范围是( )
A.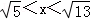 | B.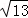 <x<5 <x<5 | C.2<x<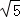 | D.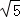 <x<5 <x<5 |
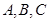 是三角形
是三角形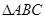 三内角,向量
三内角,向量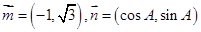 ,且
,且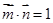
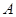 ; (2)若
; (2)若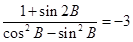 ,求
,求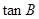 。
。