题目内容
周长为20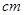 的矩形,绕一条边旋转成一个圆柱,则圆柱体积的最大值为
的矩形,绕一条边旋转成一个圆柱,则圆柱体积的最大值为
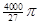

解析考点:旋转体(圆柱、圆锥、圆台).
分析:由已知中周长为20cm的矩形,绕一条边旋转成一个圆柱,我们设出圆柱的长和宽,然后可以写出圆柱体积的表达式,利用导数法,分析出体积取最大值时,自变量的值,代入即可求出圆柱体积的最大值.
解:∵矩形的周长为20cm
设矩形的长为xcm,则宽为(10-x)cm
设绕其宽旋转成一个圆柱,
则圆柱的底面半径为xcm,高为(10-x)cm
则圆柱的体积V=πR2?h=πx2(10-x)
则V′=-3πx2+20πx
令V′=0,则x=0,或x=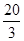
故当x=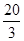 圆柱体积取最大值
圆柱体积取最大值
此时V=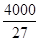 πcm3
πcm3
故答案为: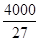 πcm3
πcm3

练习册系列答案
相关题目
 的矩形,绕一条边旋转成一个圆柱,则圆柱体积的最大值为
的矩形,绕一条边旋转成一个圆柱,则圆柱体积的最大值为