题目内容
如图,在底面是正方形的四棱锥P-ABCD中,PA⊥面ABCD,BD交AC于点E,F是PC中点,G为AC上一点.
(1)求证:BD⊥FG;
(2)确定点G在线段AC上的位置,使FG∥平面PBD,并说明理由;
(3)当二面角B-PC-D的大小为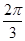 时,求PC与底面ABCD所成角的正切值
时,求PC与底面ABCD所成角的正切值

【答案】
(1)以A为原点,AB、AD、PA所在的直线分别为x、y、z轴,
建立空间直角坐标系A-xyz如图所示,

设正方形ABCD的边长为1,PA=a,则A(0,0,0),B(1,0,0),C(1,1,0),D(0,1,0),P(0,0,a)(a>0),E ,F
,F ,G(m,m,0)(0<m<
,G(m,m,0)(0<m<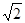 ).
).
(1) =(-1,1,0),
=(-1,1,0),
 ·
·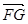 =-m+
=-m+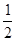 +m-
+m-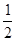 +0=0.∴BD⊥FG.
………………4分
+0=0.∴BD⊥FG.
………………4分
(2)要使FG∥平面PBD,只需FG∥EP,
由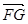 =λ
=λ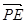 可得λ=
可得λ=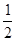 ,m=
,m=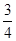 ,
,
∴ =
=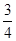
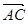 ,
,
故当AG=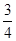 AC时,FG∥平面PBD.
………………8分
AC时,FG∥平面PBD.
………………8分
(3)设平面PBC的一个法向量为u=(x,y,z),
则,
∴取z=1,得u=(a,0,1),
同理可得平面PDC的一个法向量v=(0,a,1),
设u,v所成的角为θ,则|cosθ|=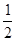 ,
,
∴a=1,
∵PA⊥面ABCD,∴∠PCA就是PC与底面ABCD所成的角,
∴tan∠PCA=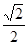 .
.
【解析】略

练习册系列答案
相关题目
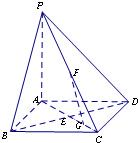 如图,在底面是正方形的四棱锥P-ABCD中,PA⊥面ABCD,BD交AC于点E,F是PC中点,G为AC上一点.
如图,在底面是正方形的四棱锥P-ABCD中,PA⊥面ABCD,BD交AC于点E,F是PC中点,G为AC上一点.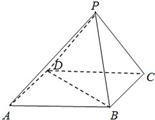 如图,在底面是正方形的四棱锥P-ABCD中,平面PCD⊥平面ABCD,PC=PD=CD=2.
如图,在底面是正方形的四棱锥P-ABCD中,平面PCD⊥平面ABCD,PC=PD=CD=2. 如图,在底面是正方形的四棱锥P-ABCD中,PA⊥面ABCD,BD交AC于点E,F是PC中点,G为AC上一点.
如图,在底面是正方形的四棱锥P-ABCD中,PA⊥面ABCD,BD交AC于点E,F是PC中点,G为AC上一点. 如图,在底面是正方形的四棱锥P-ABCD中,平面PCD⊥平面ABCD,PC=PD=CD=2.
如图,在底面是正方形的四棱锥P-ABCD中,平面PCD⊥平面ABCD,PC=PD=CD=2.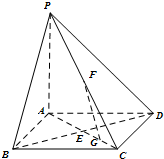 如图,在底面是正方形的四棱锥P-ABCD中,PA⊥面ABCD,BD交AC于点E,F是PC中点,G为AC上一动点.
如图,在底面是正方形的四棱锥P-ABCD中,PA⊥面ABCD,BD交AC于点E,F是PC中点,G为AC上一动点.