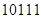题目内容
函数f(x)=
 sin2x在区间[-3,3]上的零点的个数为 ( )
sin2x在区间[-3,3]上的零点的个数为 ( )
| A.3 | B.4 | C.5 | D.6 |
B
解析试题分析:根据题意,由于函数f(x)=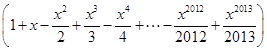
 sin2x,那么可知函数y=sin2x的零点为0,
sin2x,那么可知函数y=sin2x的零点为0,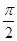 ,-
,-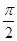 ,那么可有3个零点,同时当x=-1时
,那么可有3个零点,同时当x=-1时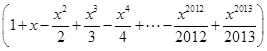 为零,故共有4个零点,答案为B.
为零,故共有4个零点,答案为B.
考点:二项式定理
点评:主要是考查了二项式定理的逆用,属于中档题。

练习册系列答案
相关题目
设三位数 ,若以
,若以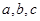 为三条边的长可以构成一个等腰(含等边)三角形,则这样的三位数
为三条边的长可以构成一个等腰(含等边)三角形,则这样的三位数 有( )
有( )
| A.45个 | B.81个 | C.165个 | D.216个 |
设函数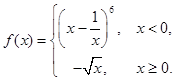 ,则当x>0时,
,则当x>0时, 表达式的展开式中常数项为
表达式的展开式中常数项为
| A.-20 | B.20 | C.-15 | D.15 |
现有16张不同的卡片,其中红色、黄色、蓝色、绿色卡片各4张.从中任取3张,要求这3张卡片不能是同一种颜色,且红色卡片至多1张.不同取法的种数为 ( )
| A.232 | B.252 | C.472 | D.484 |
若x为自然数,且 ,则
,则 等于( )
等于( )
A. | B. | C. | D. |
 的展开式中含有x的正整数幂的项的个数是
的展开式中含有x的正整数幂的项的个数是
| A.0 | B.2 | C.4 | D.6 |
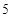 架舰载机准备着舰,如果甲、乙两机必须相邻着舰,而丙、丁两机不能相邻着舰,那么不同的着舰方法有( )
架舰载机准备着舰,如果甲、乙两机必须相邻着舰,而丙、丁两机不能相邻着舰,那么不同的着舰方法有( )


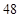
 传输信息为
传输信息为 其中
其中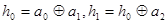 ,
,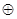 运算规则为
运算规则为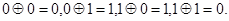 例如原信息为
例如原信息为 ,则传输信息为
,则传输信息为 ,传输信息在传输过程中受到干扰可能导致接受信息出错,则下列接受信息一定有误的是
,传输信息在传输过程中受到干扰可能导致接受信息出错,则下列接受信息一定有误的是