题目内容
有下列命题:①偶函数的图象一定与y轴相交;②奇函数的图象一定经过原点;
③定义在R上的奇函数f(x)必满足f(0)=0;
④当且仅当f(0)=0(定义域关于原点对称)时,f(x)既是奇函数又是偶函数.
其中正确的命题有 .
【答案】分析:通过举反例判断出①②错;利用奇函数的定义判断出奇函数在0处有意义函数值为0得出③对;利用奇函数、偶函数的定义判断出④对.
解答:解:对于①例如y=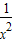 是偶函数,但图象不与y轴相交,
是偶函数,但图象不与y轴相交,
对于②例如f(x)=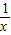 是奇函数,但图象不过原点,
是奇函数,但图象不过原点,
对于③,函数在0处有意义,f(x)为奇函数时,有f(-0)=-f(0)即f(0)=0;
对于④f(x)既是奇函数又是偶函数?f(-x)=f(x)且f(-x)=-f(x)?f(x)=-f(x)?f(x)=0,
故答案为③④
点评:本题考查奇函数、偶函数的定义及利用定义判断函数的性质;奇函数、偶函数的图象.
解答:解:对于①例如y=
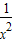 是偶函数,但图象不与y轴相交,
是偶函数,但图象不与y轴相交,对于②例如f(x)=
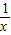 是奇函数,但图象不过原点,
是奇函数,但图象不过原点,对于③,函数在0处有意义,f(x)为奇函数时,有f(-0)=-f(0)即f(0)=0;
对于④f(x)既是奇函数又是偶函数?f(-x)=f(x)且f(-x)=-f(x)?f(x)=-f(x)?f(x)=0,
故答案为③④
点评:本题考查奇函数、偶函数的定义及利用定义判断函数的性质;奇函数、偶函数的图象.

练习册系列答案
 53随堂测系列答案
53随堂测系列答案
相关题目