题目内容
给出数字0、1、2、3、4,设由这五个数字组成的自然数的集合是A.
(1)若A中的元素a<100000,则A中共有多少个元素?
(2)已知a∈B
A,且999<a<100000,则当a的各位数字互不重复时,集合B中至多有多少个元素?
(1)若A中的元素a<100000,则A中共有多少个元素?
(2)已知a∈B
| ? | ≠ |
分析:(1)求出一位数、二位数、三位数、四位数、五位数的个数,利用分类计数原理,即可得到结论;
(2)依题意,即求由0、1、2、3、4这五个数字组成的各位数字不重复的四位数的个数
(2)依题意,即求由0、1、2、3、4这五个数字组成的各位数字不重复的四位数的个数
解答:解:(1)由于未要求各位数字不重复,∴一位数有5个,二位数有4×5=20个,三位数有4×52=100个,四位数有4×53=500个,五位数有4×54=2500个,
∴此时A中共有元素5+20+100+500+2500=3125个;
(2)依题意,即求由0、1、2、3、4这五个数字组成的各位数字不重复的四位数的个数.
∵0不能排在首位,∴这样的数共有4
=96个,
同理符合条件的五位数也有4
=96个,即B中至多有192个元素.
∴此时A中共有元素5+20+100+500+2500=3125个;
(2)依题意,即求由0、1、2、3、4这五个数字组成的各位数字不重复的四位数的个数.
∵0不能排在首位,∴这样的数共有4
| A | 3 4 |
同理符合条件的五位数也有4
| A | 3 4 |
点评:本题考查计数原理的运用,考查学生分析解决问题的能力,属于中档题.

练习册系列答案
 99加1领先期末特训卷系列答案
99加1领先期末特训卷系列答案 百强名校期末冲刺100分系列答案
百强名校期末冲刺100分系列答案 好成绩1加1期末冲刺100分系列答案
好成绩1加1期末冲刺100分系列答案 金状元绩优好卷系列答案
金状元绩优好卷系列答案
相关题目
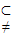 A,且999<a<100000,则当a的各位数字互不重复时,集合B中至多有多少个元素?
A,且999<a<100000,则当a的各位数字互不重复时,集合B中至多有多少个元素? 的图象关于点
的图象关于点 对称;
对称; .
.