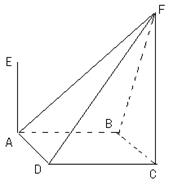
题目内容
如图所示,已知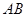 为圆
为圆 的直径,点
的直径,点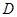 为线段
为线段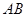 上一点,且
上一点,且 ,点
,点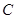 为圆
为圆 上一点,且
上一点,且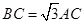 .点
.点 在圆
在圆 所在平面上的正投影为点
所在平面上的正投影为点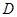 ,
, .
.
(1)求证: ;
;
(2)求二面角 的余弦值.
的余弦值.
(1)详见解析;(2)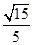
解析试题分析:(1)要证 ,需先证
,需先证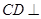 平面
平面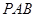 ,由于
,由于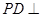 平面
平面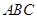 易证,故有
易证,故有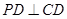 ,又因为
,又因为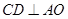 ,则证得
,则证得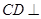 平面
平面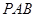 ;(2)综合法是先找到二面角的一个平面角
;(2)综合法是先找到二面角的一个平面角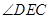 ,不过必须根据平面角的定义证明,然后在
,不过必须根据平面角的定义证明,然后在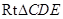 中解出
中解出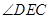 的三角函数值.
的三角函数值.
试题解析:(1)连接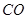 ,由
,由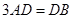 知,点
知,点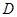 为
为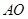 的中点,
的中点,
又∵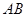 为圆
为圆 的直径,∴
的直径,∴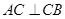 ,
,
由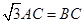 知,
知, ,
,
∴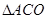 为等边三角形,从而
为等边三角形,从而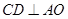 . 3分
. 3分
∵点 在圆
在圆 所在平面上的正投影为点
所在平面上的正投影为点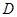 ,
,
∴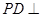 平面
平面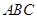 ,又
,又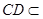 平面
平面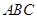 ,
,
∴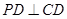 , 5分
, 5分
由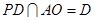 得,
得,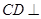 平面
平面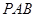 ,
,
又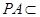 平面
平面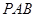 ,
,
∴ . 6分
. 6分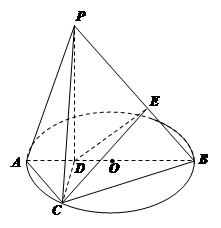
(2)(综合法)过点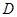 作
作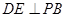 ,垂足为
,垂足为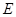 ,连接
,连接 . 7分
. 7分
由(1)知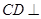 平面
平面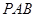 ,又
,又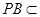 平面
平面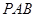 ,
,
∴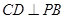 ,又
,又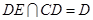 ,
,
∴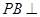 平面
平面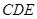 ,又
,又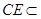 平面
平面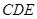 ,∴
,∴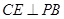 , 9分
, 9分
∴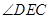 为二面角
为二面角 的平面角. 10分
的平面角. 10分
由(Ⅰ)可知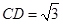 ,
, ,
,
∴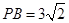 ,则
,则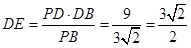 ,
,
∴在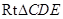 中,
中,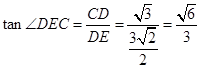 ,
,
∴ ,即二面角
,即二面角 的余弦值为
的余弦值为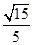 . 14分
. 14分
考点:1、线线垂直和线面垂直的证明,2、二面角的计算.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
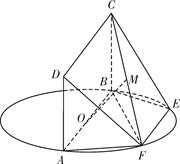
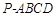 中,四边形
中,四边形 是菱形,
是菱形, ,E为PB的中点.
,E为PB的中点.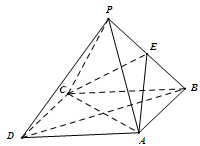
 平面
平面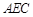 ;
;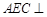 平面
平面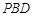 .
. 
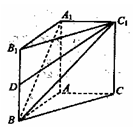
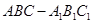 中,
中,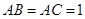 ,
,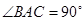 ,异面直线
,异面直线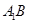 与
与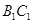 所成
所成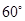 .
.
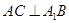 ;
;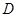 是
是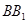 的中点,求
的中点,求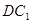 与平面
与平面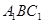 所成角的正弦值.
所成角的正弦值. 是边长为2的正三角形. 若
是边长为2的正三角形. 若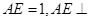 平面
平面 ,平面
,平面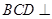 平面
平面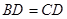 ,且
,且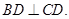
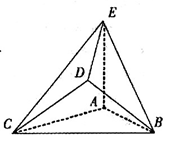
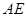 //平面
//平面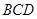 ;
; 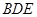
 平面
平面 .
. 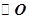 的直径,D为
的直径,D为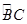 的中点,E为BC的中点.
的中点,E为BC的中点.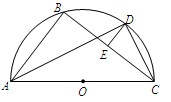
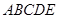 中,
中, 平面
平面 ,
,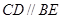 ,
,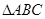 是等腰直角三角形,
是等腰直角三角形,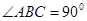 ,且
,且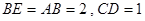 ,点
,点 是
是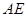 的中点.
的中点.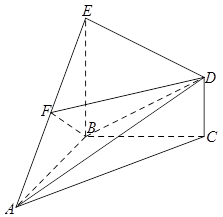
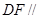 平面
平面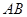 与平面
与平面 所成角的正弦值.
所成角的正弦值.  ,AE、CF都与平面ABCD垂直,AE=1,CF=2.
,AE、CF都与平面ABCD垂直,AE=1,CF=2.