题目内容
记
为一个n位正整数，其中a1，a2，…，an都是正整数，1≤a1≤9，0≤ai≤9（i=2，3，…，n）．若对任意的正整数j（1≤j≤n），至少存在另一个正整数k（1≤k≤n），使得aj=ak，则称这个数为“n位重复数”．根据上述定义，“五位重复数”的个数为． ．
【答案】分析：首先计算出从10000到99999共有90000个数，再计算出从10000到999995个数字均不相同的数有 27216个，进而得到至少有1个数字发生重复的数的个数，即可得到答案．
解答：解：由题意可得：从10000到99999共有90000个数
而从10000到99999中5个数字均不相同的数有9×9×8×7×6=27216个，
所以至少有1个数字发生重复的数共有90000-27216=62784个
所以“五位重复数”62784个．
故答案为：62784．
点评：本题主要考查排列、组合与简单计数原理的应用，要充分的运用正难则反的解题方法，解决此类问题的关键是正确理解题中所给的定义，再用所学的知识解决问题．
解答：解：由题意可得：从10000到99999共有90000个数
而从10000到99999中5个数字均不相同的数有9×9×8×7×6=27216个，
所以至少有1个数字发生重复的数共有90000-27216=62784个
所以“五位重复数”62784个．
故答案为：62784．
点评：本题主要考查排列、组合与简单计数原理的应用，要充分的运用正难则反的解题方法，解决此类问题的关键是正确理解题中所给的定义，再用所学的知识解决问题．
练习册系列答案
相关题目
为一个n位正整数，其中a1，a2，…，an都是正整数，1≤a1≤9，0≤ai≤9(i＝2，3，…，n)．若对任意的正整数j(1≤j≤n)，至少存在另一个正整数k(1≤k≤n)，使得aj＝ak，则称这个数为“n位重复数”．根据上述定义，“五位重复数”的个数为．________．
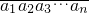为一个n位正整数，其中a1，a2，…，an都是正整数，1≤a1≤9，0≤ai≤9，（i=2，3，…，n，）．若对任意的正整数j（1≤j≤m），至少存在另一个正整数k（1≤k≤m），使得aj=ak，则称这个数为“m位重复数”．根据上述定义，“四位重复数”的个数为