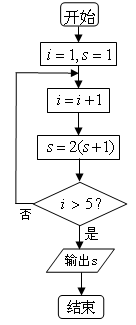
题目内容
2012年第三季度,国家电网决定对城镇居民民用电计费标准做出调整,并根据用电情况将居民分为三类:第一类的用电区间在(0,170],第二类在(170,260],第三类在(260,+∞)(单位:千瓦时.某小区共有1000户居民,现对他们的用电情况进行调查,得到频率分布直方图如图所示.
(1)求该小区居民用电量的中位数与平均数;
(2)利用分层抽样的方法从该小区内选出10位居民代表,若从该10户居民代表中任选两户居民,求这两户居民用电资费属于不同类型的概率;
(3)若该小区长期保持着这一用电消耗水平,电力部门为鼓励其节约用电,连续10个月,每个月从该小区居民中随机抽取1户,若取到的是第一类居民,则发放礼品一份,设X为获奖户数,求X的数学期望E(X)与方差D(X).

(1)求该小区居民用电量的中位数与平均数;
(2)利用分层抽样的方法从该小区内选出10位居民代表,若从该10户居民代表中任选两户居民,求这两户居民用电资费属于不同类型的概率;
(3)若该小区长期保持着这一用电消耗水平,电力部门为鼓励其节约用电,连续10个月,每个月从该小区居民中随机抽取1户,若取到的是第一类居民,则发放礼品一份,设X为获奖户数,求X的数学期望E(X)与方差D(X).

(1)∵从左边开始,前两个小矩形的面积之和为0.005×20+0.015×20=0.1+0.3=0.4<0.5,
设中位数为150+x,则0.02×x+0.4=0.5,解得x=5,∴中位数为155.
平均数为120×0.1+140×0.3+160×0.4+180×0.1+200×0.06+220×0.04=156.8;
(2)利用分层抽样的方法从该小区内选出10位居民代表,
得一类居民8户,二类居民2户,从中任取2户,共有
=45种;
两户来自不同类型的有
=16种,
∴两户居民用电资费属于不同类型的概率为
;
(3)由题意知,该小区的第一类居民占80%,
则每个月从该小区居民中随机抽取1户,取到的是第一类居民的概率为0.8,
连续10个月抽取,设X为获奖户数,则X服从二项分布,
故X的数学期望E(X)=nP=10×0.8=8,
方差D(X)=nP(1-P)=10×0.8×0.2=1.6.
设中位数为150+x,则0.02×x+0.4=0.5,解得x=5,∴中位数为155.
平均数为120×0.1+140×0.3+160×0.4+180×0.1+200×0.06+220×0.04=156.8;
(2)利用分层抽样的方法从该小区内选出10位居民代表,
得一类居民8户,二类居民2户,从中任取2户,共有
| C | 210 |
两户来自不同类型的有
| C | 18 |
| C | 12 |
∴两户居民用电资费属于不同类型的概率为
| 16 |
| 45 |
(3)由题意知,该小区的第一类居民占80%,
则每个月从该小区居民中随机抽取1户,取到的是第一类居民的概率为0.8,
连续10个月抽取,设X为获奖户数,则X服从二项分布,
故X的数学期望E(X)=nP=10×0.8=8,
方差D(X)=nP(1-P)=10×0.8×0.2=1.6.

练习册系列答案
 智趣暑假温故知新系列答案
智趣暑假温故知新系列答案 英语小英雄天天默写系列答案
英语小英雄天天默写系列答案 暑假作业安徽少年儿童出版社系列答案
暑假作业安徽少年儿童出版社系列答案
相关题目
 的分布列及期望
的分布列及期望 ,并求该商家拒收这批产品的概率.
,并求该商家拒收这批产品的概率.


 ( )
( )