题目内容
不等式2x- -a>0的在[1,2]内有实数解,则实数a的取值范围是 .
-a>0的在[1,2]内有实数解,则实数a的取值范围是 .
【答案】分析:由2x为增函数,- 是增函数,知2x-
是增函数,知2x- -a是增函数,由此能求出2x-
-a是增函数,由此能求出2x- -a在[1,2]内的最大值.
-a在[1,2]内的最大值.
解答:解:∵2x为增函数,- 是增函数,
是增函数,
所以2x- -a是增函数,
-a是增函数,
所以2x- -a在[1,2]内的最大值为2
-a在[1,2]内的最大值为2 -a=3-a>0,即a<3.
-a=3-a>0,即a<3.
故答案为:a<3.
点评:本题考查利用导数求闭区间上的函数的最值的求法,是基础题.解题时要认真审题,仔细解答,注意函数的单调性的灵活运用.本题是个存在性问题,注意转化的等价
 是增函数,知2x-
是增函数,知2x- -a是增函数,由此能求出2x-
-a是增函数,由此能求出2x- -a在[1,2]内的最大值.
-a在[1,2]内的最大值.解答:解:∵2x为增函数,-
 是增函数,
是增函数,所以2x-
 -a是增函数,
-a是增函数,所以2x-
 -a在[1,2]内的最大值为2
-a在[1,2]内的最大值为2 -a=3-a>0,即a<3.
-a=3-a>0,即a<3.故答案为:a<3.
点评:本题考查利用导数求闭区间上的函数的最值的求法,是基础题.解题时要认真审题,仔细解答,注意函数的单调性的灵活运用.本题是个存在性问题,注意转化的等价

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
 -a>0的在[1,2]内有实数解,则实数a的取值范围是________.
-a>0的在[1,2]内有实数解,则实数a的取值范围是________.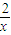 -a>0的在[1,2]内有实数解,则实数a的取值范围是 .
-a>0的在[1,2]内有实数解,则实数a的取值范围是 . -a>0的在[1,2]内有实数解,则实数a的取值范围是 .
-a>0的在[1,2]内有实数解,则实数a的取值范围是 .