Question

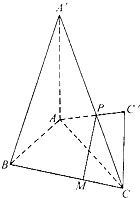如图，Rt△ABC中，∠ABC=90°，BA=BC=2，分别过A，C作平面ABC的垂线AA′和CC′，AA′=2，CC′=1，连接A′C和AC′交于点P，M为BC边上的点，CM=

2

3

．
（I）求证：直线PM∥平面A′AB；
（II）求直线MP与平面A′AC所成的角．

Answer 1

分析：（I）利用成比列线段证明 PM∥A′B，从而证明 PM∥面AA′B．
（II） PM 与面AA′C成的角即为A′B与面AA′C成的角，设AC的中点为O，∴∠BA′O 即为直线MP与平面A′AC所成的角，由tan∠BA′O=

BO

OA′

 求出∠BA′O 的大小．

解答：解：（I）证明：∵AA′⊥平面ABC，∴CC′⊥平面ABC，∴AA′∥CC′，∴

A′P

PC

= 

A′A

C′C

 = 

2

1

．
又∵CM=

2

3

，BC=2，∴

BM

MC

=2，∴PM∥A′B．又 A′B?面AA′B，
PM不在面AA′B内，∴PM∥面AA′B．
（II）由（I）知，PM∥A′B，∴PM 与面AA′C成的角即为A′B与面AA′C成的角，设AC的中点为O，
Rt△ABC中，BA=BC=2，∴BO⊥AC，且 BO=

2

．∵AA′⊥面ABC，∴面AA′C⊥面ABC，
又∵面AA′C∩面ABC=AC，∴BO⊥面ABC，∴∠BA′O 即为直线MP与平面A′AC所成的角．
∵AO=

2

，A′A=2，∴A′O=

6

，∴tan∠BA′O=

BO

OA′

=

3

3

，∴∠BA′O=30°．
故直线MP与平面A′AC所成的角为30°．

点评：本题考查证明线面平行的方法，求直线和平面成的角，找出直线和平面成的角是解题的关键．