题目内容
若数列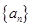 满足
满足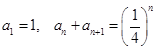 ,设
,设 ,
,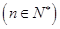 ,类比课本中推导等比数列前
,类比课本中推导等比数列前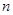 项和公式的方法,可求得
项和公式的方法,可求得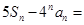 .
.
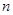
解析试题分析:由题意,Sn=a1+a2×4+a3×42+…+an×4n-1,①
两边同乘以4,得
4Sn=a1×4+a2×42+…+an-1×4n-1+an×4n,②
由①+②,得
5Sn=a1+(a1+a2)×4+(a2+a3)×42+…+(an-1+an)×4n-1+an×4n,
又a1=1,an+an+1=()n,
所以a1+a2=,a2+a3=()2,…,
所以5Sn=1+1+1+…+1,\s\do4(共n个))+an×4n,故5Sn-4nan=n.
考点:类比推理.

练习册系列答案
 提分百分百检测卷单元期末测试卷系列答案
提分百分百检测卷单元期末测试卷系列答案 小学期末标准试卷系列答案
小学期末标准试卷系列答案
相关题目
已知数列{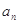 }满足
}满足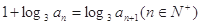 ,且
,且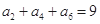 ,则
,则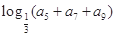 的值是 ( )
的值是 ( )
A.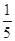 | B.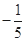 | C.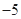 | D.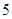 |
 的通项公式
的通项公式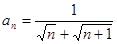 ,则该数列的前_________项之和等于
,则该数列的前_________项之和等于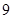 .
.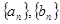 都是公差为1的等差数列,其首项分别为
都是公差为1的等差数列,其首项分别为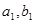 ,且
,且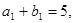
 设
设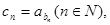 则数列
则数列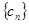 的前10项和等于______.
的前10项和等于______.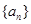 的前
的前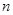 项的和为
项的和为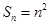 ,则
,则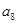 =_________.
=_________.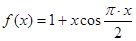 ,则
,则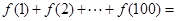 .
.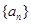 满足
满足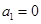 ,
,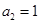 ,
,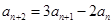 ,则
,则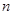 项和
项和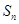 = .
= . 的前
的前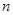 项和
项和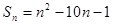
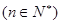 ,则此数列的通项公式为 .
,则此数列的通项公式为 .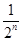 ,n∈N?,则a3=________.
,n∈N?,则a3=________.