题目内容
已知c为常数,s2=| 1 |
| n |
. |
| x |
. |
| x |
. |
| x |
| 1 |
| n |
. |
| x |
分析:证明sc2≥s2,可证明sc2-s2≥0.因此应用方差公式进行变形得到完全平方式即可得到大于等于0.
解答:证明:∵
=
,
∴s2=
[(x1-
)2+…+(xn-
)2]=
[(x12+x22+…+xn2)-2
(x1+x2+…+xn)+n
2]=
[(x12+x22+…+xn2)-n
2],
sc2=
[(x1-c)2+(x2-c)2+…+(xn-c)2]=
[(x12+x22+…+xn2)-2c(x1+x2+…+xn)+nc2],
∴sc2-s2=
2-
(x1+x2+…+xn)+c2
=
2-2c•
+c2=(
-c)2≥0.
∴sc2≥s2,当且仅当
=c时取“=”.
. |
| x |
| x1+x2+…+xn |
| n |
∴s2=
| 1 |
| n |
. |
| x |
. |
| x |
| 1 |
| n |
. |
| x |
. |
| x |
| 1 |
| n |
. |
| x |
sc2=
| 1 |
| n |
| 1 |
| n |
∴sc2-s2=
. |
| x |
| 2c |
| n |
=
. |
| x |
. |
| x |
. |
| x |
∴sc2≥s2,当且仅当
. |
| x |
点评:本题考查学生会求一组数据的平均数、方差.学生证明时,掌握作差是比较大小的常用手段.

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
 [(x1-
[(x1- )2+(x2-
)2+(x2-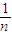 [(x1-
[(x1- )2+(x2-
)2+(x2- )2+…+(xn-
)2+…+(xn-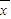 )2],sc2=
)2],sc2=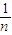 [(x1-c)2+(x2-c)2+…+(xn-c)2].证明:s2≤sc2,当且仅当c=
[(x1-c)2+(x2-c)2+…+(xn-c)2].证明:s2≤sc2,当且仅当c=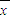 时,取“=”.
时,取“=”.