题目内容
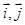 是两个不共线向量,已知
是两个不共线向量,已知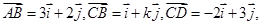 若
若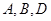 三点共线,则实数
三点共线,则实数 的值为
的值为
5;
解析试题分析:因为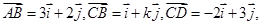 所以
所以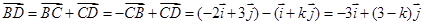
因为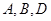 三点共线,所以3×(3-k)-2×(-3)=0,k=5.
三点共线,所以3×(3-k)-2×(-3)=0,k=5.
考点:本题主要考查向量的线性运算,共线点的确定方法。
点评:证明三点共线的方法是,先证明相关向量共线。三点共线,则相关向量共线,对应坐标成比例。

练习册系列答案
 世纪百通主体课堂小学课时同步达标系列答案
世纪百通主体课堂小学课时同步达标系列答案 世纪百通优练测系列答案
世纪百通优练测系列答案 百分学生作业本题练王系列答案
百分学生作业本题练王系列答案
相关题目
题目内容
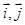 是两个不共线向量,已知
是两个不共线向量,已知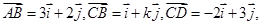 若
若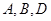 三点共线,则实数
三点共线,则实数 的值为
的值为
5;
解析试题分析:因为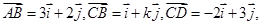 所以
所以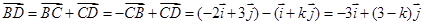
因为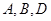 三点共线,所以3×(3-k)-2×(-3)=0,k=5.
三点共线,所以3×(3-k)-2×(-3)=0,k=5.
考点:本题主要考查向量的线性运算,共线点的确定方法。
点评:证明三点共线的方法是,先证明相关向量共线。三点共线,则相关向量共线,对应坐标成比例。

 世纪百通主体课堂小学课时同步达标系列答案
世纪百通主体课堂小学课时同步达标系列答案 世纪百通优练测系列答案
世纪百通优练测系列答案 百分学生作业本题练王系列答案
百分学生作业本题练王系列答案