题目内容
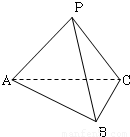
如图所示三棱锥P-ABC中，异面直线PA与BC所成的角为90°，二面角P-BC-A为60°，△PBC和△ABC的面积分别为16和10，BC=4．求：（1）PA的长；
（2）三棱锥P-ABC的体积VP-ABC．
分析：（1）作AD⊥BC于D，连PD，说明∠PDA为二面角的平面角，求出PD，AD，然后利用余弦定理，求出PA．
（2）求出三角形PAD的面积与BC乘积的
，即可得到几何体的体积．
（2）求出三角形PAD的面积与BC乘积的
| 1 |
| 3 |
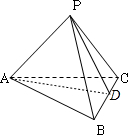
解答：解：（1）作AD⊥BC于D，连PD，由已知PA⊥BC，∴BC⊥面PAD，∴BC⊥PD，∴∠PDA为二面角
的平面角，∴∠PDF=60°，可算出PD=8，AD=5，∴PA=
=7．
（2）V=
×
PD•ADsin60°•BC=
×
×8×5×
×4=
的平面角，∴∠PDF=60°，可算出PD=8，AD=5，∴PA=
| AD2+DP2-2AD•PDcos60° |
（2）V=
| 1 |
| 3 |
| 1 |
| 2 |
| 1 |
| 3 |
| 1 |
| 2 |
| ||
| 2 |
40
| ||
| 3 |
点评：本题考查异面直线所成的角，二面角，几何体的体积的求法，余弦定理的应用，考查空间想象能力，计算能力．
练习册系列答案
相关题目
，D为BC的中点，E为AP的中点．P在底面△ABC内的射影为O，以O为坐标原点，OD、OP所在直线分别为Y、Z轴建立如图所示的空间直角坐标系O－XYZ．
，D为BC的中点，E为AP的中点．P在底面△ABC内的射影为O，以O为坐标原点，OD、OP所在直线分别为Y、Z轴建立如图所示的空间直角坐标系O－XYZ．
，二面角P—BC—A为
，△PBC和△ABC的面积分别为16和10，BC＝４. 求：
（１）PA的长；（２）三棱锥P—ABC的体积
