题目内容
在直角坐标系中,有一点列P1(a1,b1),P2(a2,b2),…,Pn(an,bn),…对每一个正整数n,点Pn在给定的函数,y=log3(2x)的图象上,点Pn和点((n-1,0)与点(n,0)构成一个以Pn为顶点的等腰三角形.(I) 求点Pn的纵坐标bn的表达式;
(II) 记cn=
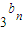 ,n∈N+.
,n∈N+.①证明
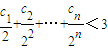 ;
;②是否存在实数k,使得
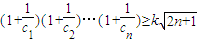 对一切n∈N+均成立,若存在,求出的最大值;若不存在,说明理由.
对一切n∈N+均成立,若存在,求出的最大值;若不存在,说明理由.
【答案】分析:(Ⅰ)由题意可得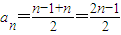 ,然后由点Pn在给定的函数,y=log3(2x)的图象可求bn
,然后由点Pn在给定的函数,y=log3(2x)的图象可求bn
(Ⅱ)①由cn= =2n-1,然后利用错位相减求和方法可求
=2n-1,然后利用错位相减求和方法可求 ,然后进行证明
,然后进行证明
②由k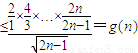 恒成立,要求k的范围,利用函数的单调性求解g(n)的最小值,从而k≤g(n)的最小值,即可求解k的范围
恒成立,要求k的范围,利用函数的单调性求解g(n)的最小值,从而k≤g(n)的最小值,即可求解k的范围
解答:解:(Ⅰ)∵Pn(an,bn),(n-1,0)与点(n,0)构成一个以Pn为顶点的等腰三角形
∴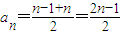 …(2分)
…(2分)
又因为点Pn在给定的函数,y=log3(2x)的图象
∴bn=log3(2n-1)…(4分)
(Ⅱ)①∵cn= =2n-1------------------(5分)
=2n-1------------------(5分)
设Dn=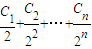
则Dn= ①
①
∴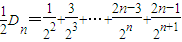 ②…(6分)
②…(6分)
由①-②得: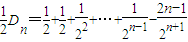
∴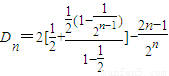
=1+2-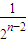

=3-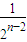
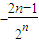 <3--------(9分)
<3--------(9分)
②由已知得k 对一切n∈N+均成立.
对一切n∈N+均成立.
∴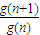 =
=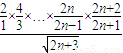 ×
×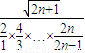
=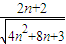 =
=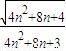 >1-------(12分)
>1-------(12分)
∴g(n)单调递增.最小值为g(1)=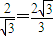 --------(13分)
--------(13分)
又∵k≤g(n)对一切n∈N+均成立.
∴k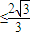 .
.
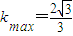 …(14分)
…(14分)
点评:本题主要考查了数列的递推公式的应用,错位相减求和方法的应用,及函数的单调性在求解函数的最值中的应用,函数的恒成立与函数最值求解的相互转化.
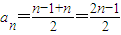 ,然后由点Pn在给定的函数,y=log3(2x)的图象可求bn
,然后由点Pn在给定的函数,y=log3(2x)的图象可求bn(Ⅱ)①由cn=
 =2n-1,然后利用错位相减求和方法可求
=2n-1,然后利用错位相减求和方法可求 ,然后进行证明
,然后进行证明②由k
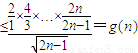 恒成立,要求k的范围,利用函数的单调性求解g(n)的最小值,从而k≤g(n)的最小值,即可求解k的范围
恒成立,要求k的范围,利用函数的单调性求解g(n)的最小值,从而k≤g(n)的最小值,即可求解k的范围解答:解:(Ⅰ)∵Pn(an,bn),(n-1,0)与点(n,0)构成一个以Pn为顶点的等腰三角形
∴
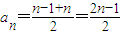 …(2分)
…(2分)又因为点Pn在给定的函数,y=log3(2x)的图象
∴bn=log3(2n-1)…(4分)
(Ⅱ)①∵cn=
 =2n-1------------------(5分)
=2n-1------------------(5分)设Dn=
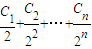
则Dn=
 ①
①∴
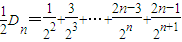 ②…(6分)
②…(6分)由①-②得:
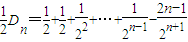
∴
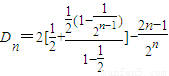
=1+2-
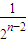

=3-
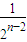
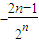 <3--------(9分)
<3--------(9分)②由已知得k
 对一切n∈N+均成立.
对一切n∈N+均成立.∴
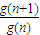 =
=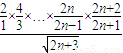 ×
×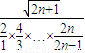
=
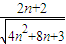 =
=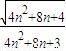 >1-------(12分)
>1-------(12分)∴g(n)单调递增.最小值为g(1)=
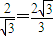 --------(13分)
--------(13分)又∵k≤g(n)对一切n∈N+均成立.
∴k
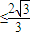 .
.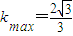 …(14分)
…(14分)点评:本题主要考查了数列的递推公式的应用,错位相减求和方法的应用,及函数的单调性在求解函数的最值中的应用,函数的恒成立与函数最值求解的相互转化.

练习册系列答案
相关题目
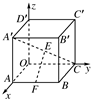 如图所示,在空间直角坐标系中,有一棱长为a的正方体ABCO-A′B′C′D′,A′C的中点E与AB的中点F的距离为( )
如图所示,在空间直角坐标系中,有一棱长为a的正方体ABCO-A′B′C′D′,A′C的中点E与AB的中点F的距离为( )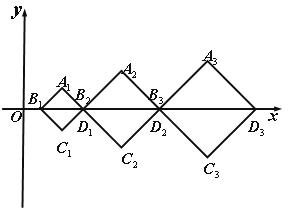
 (3)若
(3)若