题目内容
已知函数 ,现给出下列命题:
,现给出下列命题:①当图象是一条连续不断的曲线时,则a=
 ;
;②当图象是一条连续不断的曲线时,能找到一个非零实数a,使得f (x)在R上是增函数;
③当
 时,不等式f(1+a)•f(1-a)<0恒成立;
时,不等式f(1+a)•f(1-a)<0恒成立;④函数 y=f(|x+1|)是偶函数.
其中正确的命题是( )
A.①③
B.②④
C.①③④
D.①②③④
【答案】分析: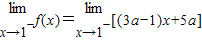 =8a-1=
=8a-1=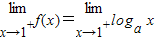 =0⇒a=
=0⇒a= ,故①正确;a=
,故①正确;a= ,f (x)在R上是减函数,故②不正确;当
,f (x)在R上是减函数,故②不正确;当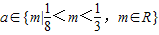 时,不等式f(1+a)•f(1-a)<0恒成立,故③正确;函数 y=f(|x+1|)是偶函数不成立.即④不正确.
时,不等式f(1+a)•f(1-a)<0恒成立,故③正确;函数 y=f(|x+1|)是偶函数不成立.即④不正确.
解答:解: =8a-1,
=8a-1,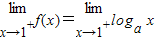 =0,
=0,
∵图象是一条连续不断的曲线,
∴8a-1=0,a= ,故①正确;
,故①正确;
当图象是一条连续不断的曲线时,
a= ,f (x)在R上是减函数,故②不正确;
,f (x)在R上是减函数,故②不正确;
当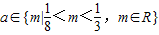 时,
时,
不等式f(1+a)•f(1-a)<0恒成立,故③正确;
函数 y=f(|x+1|)是偶函数不成立.即④不正确.
故选A.
点评:本题考查命题的真假判断与应用,解题时要注意极限和连续的合理运用.
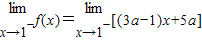 =8a-1=
=8a-1=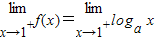 =0⇒a=
=0⇒a= ,故①正确;a=
,故①正确;a= ,f (x)在R上是减函数,故②不正确;当
,f (x)在R上是减函数,故②不正确;当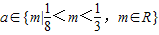 时,不等式f(1+a)•f(1-a)<0恒成立,故③正确;函数 y=f(|x+1|)是偶函数不成立.即④不正确.
时,不等式f(1+a)•f(1-a)<0恒成立,故③正确;函数 y=f(|x+1|)是偶函数不成立.即④不正确.解答:解:
 =8a-1,
=8a-1,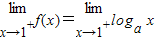 =0,
=0,∵图象是一条连续不断的曲线,
∴8a-1=0,a=
 ,故①正确;
,故①正确;当图象是一条连续不断的曲线时,
a=
 ,f (x)在R上是减函数,故②不正确;
,f (x)在R上是减函数,故②不正确;当
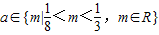 时,
时,不等式f(1+a)•f(1-a)<0恒成立,故③正确;
函数 y=f(|x+1|)是偶函数不成立.即④不正确.
故选A.
点评:本题考查命题的真假判断与应用,解题时要注意极限和连续的合理运用.

练习册系列答案
相关题目
 ,现给出下列命题:
,现给出下列命题: =
= ;
; 在
在 上是增函数;
上是增函数;  时,不等式
时,不等式 恒成立;
恒成立; 是偶函数.
是偶函数. ,现给出下列命题:
,现给出下列命题: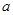 =
= ;
;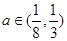 时,不等式
时,不等式 恒成立
恒成立 是偶函数
是偶函数 ,现给出下列命题:
,现给出下列命题: =
=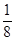 ;
; 时,不等式
时,不等式 恒成立;
恒成立;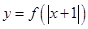 是偶函数 . 其中正确的命题是 ( )
是偶函数 . 其中正确的命题是 ( )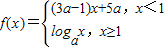 ,现给出下列命题:
,现给出下列命题: ;
;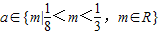 时,不等式f(1+a)•f(1-a)<0恒成立;
时,不等式f(1+a)•f(1-a)<0恒成立;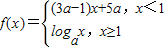 ,现给出下列命题:
,现给出下列命题: ;
;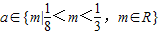 时,不等式f(1+a)•f(1-a)<0恒成立;
时,不等式f(1+a)•f(1-a)<0恒成立;