题目内容
在△ 中,角
中,角 所对的边分别为
所对的边分别为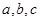 ,且满足
,且满足 ,则
,则 的最大值是( )
的最大值是( )
A. | B.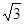 | C. | D.2 |
A
解析试题分析:因为 ,根据正弦定理,有
,根据正弦定理,有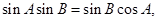
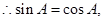
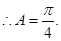
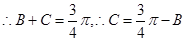 ,
,
所以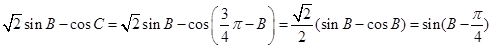 ,所以最大值为
,所以最大值为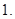
考点:本小题主要考查正弦定理、三角形内角和定理、两角差的余弦公式和辅助角公式、最值的求解和应用,考查学生综合运用公式的能力和数形结合考查三角函数性质的能力.
点评:要考查三角函数的性质,应该先把函数化为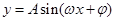 的形式.
的形式.

练习册系列答案
 文敬图书课时先锋系列答案
文敬图书课时先锋系列答案
相关题目
在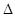 ABC中,
ABC中,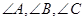 所对的边分别为a,b,c,已知a=2,b=
所对的边分别为a,b,c,已知a=2,b=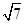 ,
,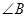 =
= ,则
,则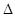 ABC的面积为
ABC的面积为
A.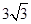 | B.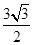 | C. | D.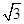 |
已知 中,
中, 则
则 等于( )
等于( )
A. | B. | C. | D. |
在 中,已知
中,已知 ,则
,则
A. | B. | C. | D. |
在△ 中,内角
中,内角 的对边分别为
的对边分别为 。若
。若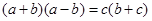 ,则
,则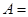
A.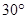 | B.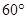 | C.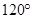 | D.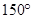 |
在△ABC中,若 ,则△ABC的形状是( )
,则△ABC的形状是( )
| A.直角三角形 | B.等边三角形 | C.等腰三角形 | D.不能确定 |
在△ 中,若
中,若 ,则△
,则△ 的形状是( )
的形状是( )
| A.锐角三角形 | B.直角三角形 |
| C.钝角三角形 | D.不能确定 |
在 中,
中, ,则此三角形解的情况是 ( )
,则此三角形解的情况是 ( )
| A.一解 | B.两解 | C.一解或两解 | D.无解 |
 ,则△ABC的面积S =
,则△ABC的面积S =