题目内容
给定下列命题
①半径为2,圆心角的弧度数为
的扇形的面积为
;
②若a、β为锐角,tan(α+β)=
,tanβ=
,则α+2β=
;
③若A、B是△ABC的两个内角,且sinA<sinB,则BC<AC;
④若a、b、c分别是△ABC的三个内角A、B、C所对边的长,且a2+b2-c2<0,则△ABC一定是钝角三角形.
其中正确命题的个数有( )
①半径为2,圆心角的弧度数为
| 1 |
| 2 |
| 1 |
| 2 |
②若a、β为锐角,tan(α+β)=
| 1 |
| 3 |
| 1 |
| 2 |
| π |
| 4 |
③若A、B是△ABC的两个内角,且sinA<sinB,则BC<AC;
④若a、b、c分别是△ABC的三个内角A、B、C所对边的长,且a2+b2-c2<0,则△ABC一定是钝角三角形.
其中正确命题的个数有( )
分析:①计算扇形面积,②计算tan(α+2β)的值,考虑α,β的范围,③△ABC中,sinA<sinB,得A<B,得BC<AC,④△ABC中,a2+b2-c2<0,得cosC<0,得C是钝角.
解答:解:①半径为2,圆心角的弧度数为
的扇形的面积为:S=
R2α=
×22×
=1,∴①错误;
②若a、β为锐角,tan(α+β)=
,tanβ=
,则tan(α+2β)=
=
=1,
∵0<α<
,0<β<
,且tan(α+β)=
,∴0<α+β<
,∴0<α+2β<π,∴α+2β=
,∴②正确;
③若A、B是△ABC的两个内角,且sinA<sinB,则A<B,由大角对大边知BC<AC,∴③正确;
④若a、b、c分别是△ABC的三个内角A、B、C所对边的长,且a2+b2-c2<0,
∴cosC=
<0,又0<C<π,∴C是钝角,即△ABC是钝角三角形,∴④正确.
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |
②若a、β为锐角,tan(α+β)=
| 1 |
| 3 |
| 1 |
| 2 |
| tan(α+β)+tanβ |
| 1-tan(α+β)tanβ |
| ||||
1-
|
∵0<α<
| π |
| 2 |
| π |
| 2 |
| 1 |
| 3 |
| π |
| 2 |
| π |
| 4 |
③若A、B是△ABC的两个内角,且sinA<sinB,则A<B,由大角对大边知BC<AC,∴③正确;
④若a、b、c分别是△ABC的三个内角A、B、C所对边的长,且a2+b2-c2<0,
∴cosC=
| a2+b2-c2 |
| 2ab |
点评:本题考查了扇形面积公式,两角和的正切公式,三角形中正弦、余弦定理的综合应用,是容易出错的基础题.

练习册系列答案
相关题目
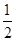 的扇形的面积为
的扇形的面积为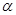 、
、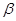 为锐角,
为锐角,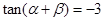 ,
,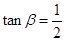 ,则
,则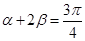 ;
; 、
、 是△
是△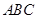 的两个内角,且
的两个内角,且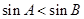 ,则
,则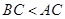 ;
;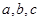 分别是△
分别是△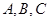 所对边的长,
所对边的长,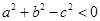 ,则△
,则△ 的扇形的面积为
的扇形的面积为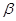 为锐角,
为锐角,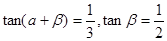 ,则
,则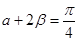 ;
;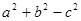 <0
<0 的扇形的面积为
的扇形的面积为 为锐角,
为锐角, ,则
,则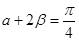 ;
;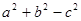 <0
<0