题目内容
制造甲、乙两种烟花,甲种烟花每枚含A药品3 g、B药品4 g、C药品4 g,乙种烟花每枚含A药品2 g、B药品11 g、C药品6 g.已知每天原料的使用限额为A药品120 g、B药品400 g、C药品240 g,甲种烟花每枚可获利1.2美元,乙种烟花每枚可获利1美元,问每天应生产甲、乙两种烟花各多少枚才能获利最大?
解:根据题意,可列出下表:
| A药品(g) | B药品(g) | C药品(g) |
甲种烟花 | 3 | 4 | 4 |
乙种烟花 | 2 | 11 | 6 |
原料限额 | 120 | 400 | 240 |
设每天生产甲种烟花x枚、乙种烟花y枚,获利为z美元,则目标函数z=1.2x+y(美元).
其中x、y应满足:
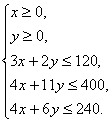
作出上面的不等式组所表示的平面区域如下图所示.
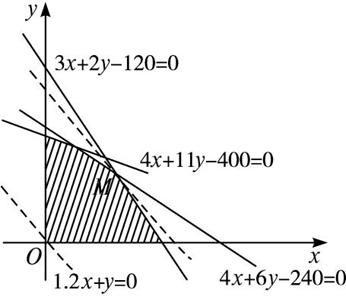
把z=1.2x+y变形为平行直线系l:y=-1.2x+z.
由图可知,当直线l经过平面区域上的点M时,截距z最大.
解方程组![]()
得交点M(24,24).
故每天生产甲种烟花24枚、乙种烟花24枚,能使利润最大.

练习册系列答案
相关题目