题目内容
(本小题满分12分)在数列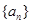 中,
中, ,并且对于任意n∈N*,都有
,并且对于任意n∈N*,都有 .
.
(1)证明数列 为等差数列,并求
为等差数列,并求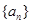 的通项公式;
的通项公式;
(2)设数列 的前n项和为
的前n项和为 ,求使得
,求使得 的最小正整数
的最小正整数 .
.
(1)  (2) 91
(2) 91
解析试题分析:解:(1)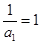 ,因为
,因为 ,所以
,所以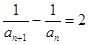 ,
,
∴ 数列 是首项为1,公差为2的等差数列,
是首项为1,公差为2的等差数列,
∴ 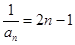 ,从而
,从而 ………… ……………………………6分
………… ……………………………6分
(2) 因为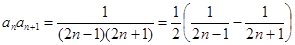
所以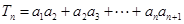
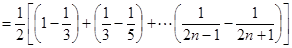
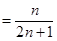 ,
,
由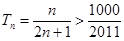 ,
,
得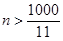 ,
,
最小正整数 为91.………………………………………………12分
为91.………………………………………………12分
考点:本试题考查了数列的通项公式和求和的运用。
点评:对于已知等差数列和等比数列的通项公式的求解,主要是求解两个基本元素,解方程组得到结论。而对于一般的数列求和思想,主要是分析其通项公式的特点,选择是用错位相减法还是裂项法,还是倒序相加法等等的求和方法来得到。属于中档题。

练习册系列答案
 暑假作业海燕出版社系列答案
暑假作业海燕出版社系列答案 本土教辅赢在暑假高效假期总复习云南科技出版社系列答案
本土教辅赢在暑假高效假期总复习云南科技出版社系列答案 暑假作业北京艺术与科学电子出版社系列答案
暑假作业北京艺术与科学电子出版社系列答案
相关题目
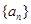 中,
中,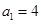 ,
, 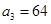 .
.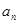 ;
; 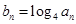 ,求数列
,求数列 的前n项和
的前n项和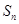 ;
;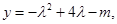 对于(2)中的
对于(2)中的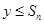 对一切正整数n及任意实数
对一切正整数n及任意实数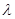 恒成立,求实数m的取值范围.
恒成立,求实数m的取值范围. 对任意
对任意 ,满足
,满足 (
( 为常数),称数列
为常数),称数列 项和
项和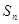 满足
满足 ,求
,求 ,数列
,数列 的前
的前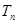 , 求证:
, 求证: .
. 中,
中,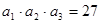 ,
,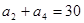
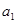 和公比
和公比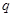 ; (Ⅱ)前6项的和
; (Ⅱ)前6项的和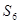 .
.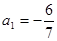 ,
, (其中λ≠0且λ≠–1,n∈N*),
(其中λ≠0且λ≠–1,n∈N*),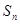 为数列{an}的前
为数列{an}的前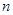 项和.
项和.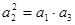 ,求
,求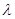 的值;
的值;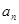 ;
;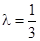 时,数列{an}中是否存在三项构成等差数列,若存在,请求出此三项;若不存在,请说明理由.
时,数列{an}中是否存在三项构成等差数列,若存在,请求出此三项;若不存在,请说明理由.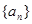 ,
,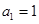 ,
,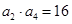 ,单调增数列
,单调增数列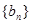 的前
的前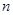 项和为
项和为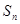 ,
,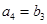 ,且
,且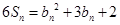 (
(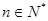 ).
).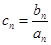 (
(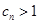 的所有
的所有 对任意正整数n都成立,m为大于—1的非零常数。
对任意正整数n都成立,m为大于—1的非零常数。 是等比数列;
是等比数列;




 满足 ,
满足 , ,(
,( )
) +
+ +
+ +…+
+…+ =( )
=( )


