题目内容
A高校自主招生设置了先后三道程序:部分高校联合考试、本校专业考试、本校面试.在每道程序中,设置三个成绩等级:优、良、中.若考生在某道程序中获得“中”,则该考生在本道程序中不通过,且不能进入下面的程序.考生只有全部通过三道程序,自主招生考试才算通过.某中学学生甲参加A高校自主招生考试,已知该生在每道程序中通过的概率均为 ,每道程序中得优、良、中的概率分别为p1、
,每道程序中得优、良、中的概率分别为p1、 、p2.
、p2.
(1)求学生甲不能通过A高校自主招生考试的概率;
(2)设X为学生甲在三道程序中获优的次数,求X的概率分布及数学期望.
 ,每道程序中得优、良、中的概率分别为p1、
,每道程序中得优、良、中的概率分别为p1、 、p2.
、p2.(1)求学生甲不能通过A高校自主招生考试的概率;
(2)设X为学生甲在三道程序中获优的次数,求X的概率分布及数学期望.
(1)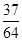 (2)X的概率分布为:
(2)X的概率分布为:
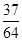
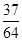 (2)X的概率分布为:
(2)X的概率分布为:| X | 0 | 1 | 2 | 3 |
| P | 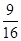 |  | 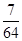 | 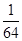 |
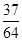
解:由题意,得
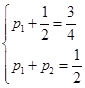 解得p1=p2=
解得p1=p2= .
.(1)设事件A为学生甲不能通过A高校自主招生考试,则P(A)=
 +
+ ×
× +
+ ×
× ×
× =
=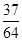 .
.即学生甲不能通过A高校自主招生考试的概率为
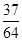 .
.(2)由题意知,X=0,1,2,3.
P(X=0)=
 +
+ ×
× +
+ ×
× ×
× +
+ ×
× ×
× =
=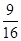 ,
,P(X=2)=
 ×
× ×
× +
+ ×
× ×
× +
+ ×
× ×
× +
+ ×
× ×
× =
=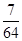 ,P(X=3)=
,P(X=3)= ×
× ×
× =
=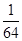 ,
,∵
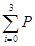 (X=i)=1,
(X=i)=1,∴P(X=1)=1-P(X=0)-P(X=2)-P(X=3)=
 .
.∴X的概率分布为:
| X | 0 | 1 | 2 | 3 |
| P | 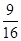 |  | 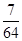 | 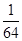 |
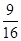 +1×
+1× +2×
+2×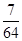 +3×
+3×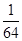 =
=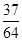 .
.
练习册系列答案
相关题目
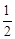 ,从陆路每个方向抵达灾区的概率都是
,从陆路每个方向抵达灾区的概率都是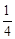 .
.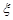 的数学期望.
的数学期望.
 名学生被考官L面试,求
名学生被考官L面试,求
 (
( ≥0)万元,投资B项目资金为
≥0)万元,投资B项目资金为 (
( ≥0)万元,调研结果是:未来一年内,位于一类风区的A项目获利
≥0)万元,调研结果是:未来一年内,位于一类风区的A项目获利 的可能性为
的可能性为 ,亏损
,亏损 的可能性为
的可能性为 ;位于二类风区的B项目获利
;位于二类风区的B项目获利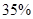 的可能性为
的可能性为 的可能性是
的可能性是 ,不赔不赚的可能性是
,不赔不赚的可能性是 .
. 和
和 ,试写出随机变量
,试写出随机变量 ,
, ;
; 万元的资金投资于A,B项目,且公司要求对A项目的投
万元的资金投资于A,B项目,且公司要求对A项目的投 的最大值.
的最大值.
 表示抽到“极幸福”的人数,求
表示抽到“极幸福”的人数,求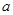 个红球,
个红球,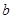 个黄球,
个黄球,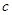 个蓝球,且规定:取出一个红球得1分,
个蓝球,且规定:取出一个红球得1分,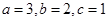 时,从该袋子中任取(有放回,且每球取到的机会均等)2个球,记随机变量
时,从该袋子中任取(有放回,且每球取到的机会均等)2个球,记随机变量 为取出此2球所得分数之和,.求
为取出此2球所得分数之和,.求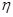 为取出此球所得分数.若
为取出此球所得分数.若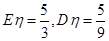 ,求
,求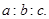
 ,则方差V(X)的值是________.
,则方差V(X)的值是________.