题目内容
 在海岸A处,发现北偏东45°方向,距离A为(
在海岸A处,发现北偏东45°方向,距离A为(| 3 |
| 3 |
分析:在△ABC中,∠CAB=120°由余弦定理可求得线段BC的长度;在△ABC中,由正弦定理,可求得sin∠ACB;设缉私船用t h在D处追上走私船,CD=10
t,BD=10t,在△ABC中,可求得∠CBD=120°,再在△BCD中,由正弦定理可求得sin∠BCD,从而可求得缉私艇行驶方向,在△BCD中易判断BD=BC,由t=
即可得到追缉时间.
| 3 |
| BD |
| 10 |
解答: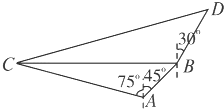 解:在△ABC中,∠CAB=45°+75°=120°,
解:在△ABC中,∠CAB=45°+75°=120°,
由余弦定理,得BC2=AB2+AC2-2AB•ACcos∠CAB
=(
-1)2+22-2×(
-1)×2×(-
)=6,
所以,BC=
.
在△ABC中,由正弦定理,得
=
,
所以,sin∠ACB=
=
=
.
又∵0°<∠ACB<60°,∴∠ACB=15°.
设缉私船用t h在D处追上走私船,如图,
则有CD=10
t,BD=10t.
又∠CBD=90°+30°=120°,
在△BCD中,由正弦定理,得
sin∠BCD=
=
=
.
∴∠BCD=30°,
又因为∠ACB=15°,
所以1800-(∠BCD+∠ACB+75°)=180°-(30°+15°+75°)=60°,
即缉私船沿北偏东60°方向能最快追上走私船.?
在△BCD中,∴∠BCD=30°,∠CBD=90°+30°=120°,
∴∠CDB=30°,∴BD=BC=
,
则t=
,即缉私艇最快追上走私船所需时间
h.
 解:在△ABC中,∠CAB=45°+75°=120°,
解:在△ABC中,∠CAB=45°+75°=120°,由余弦定理,得BC2=AB2+AC2-2AB•ACcos∠CAB
=(
| 3 |
| 3 |
| 1 |
| 2 |
所以,BC=
| 6 |
在△ABC中,由正弦定理,得
| AB |
| sin∠ACB |
| BC |
| sin120° |
所以,sin∠ACB=
| AB•sin120° |
| BC |
| ||
2
|
| ||||
| 4 |
又∵0°<∠ACB<60°,∴∠ACB=15°.
设缉私船用t h在D处追上走私船,如图,
则有CD=10
| 3 |
又∠CBD=90°+30°=120°,
在△BCD中,由正弦定理,得
sin∠BCD=
| BD•sin∠CBD |
| CD |
| 10t•sin120° | ||
10
|
| 1 |
| 2 |
∴∠BCD=30°,
又因为∠ACB=15°,
所以1800-(∠BCD+∠ACB+75°)=180°-(30°+15°+75°)=60°,
即缉私船沿北偏东60°方向能最快追上走私船.?
在△BCD中,∴∠BCD=30°,∠CBD=90°+30°=120°,
∴∠CDB=30°,∴BD=BC=
| 6 |
则t=
| ||
| 10 |
| ||
| 10 |
点评:本题考查余弦定理与正弦定理在解决实际问题中的应用,考查解三角形,考查综合分析与运算能力,属于难题.

练习册系列答案
相关题目
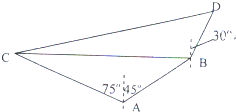 在海岸A处,发现北偏东45°方向,距A处(
在海岸A处,发现北偏东45°方向,距A处( 在海岸A处,发现北偏东45°方向,距离A
在海岸A处,发现北偏东45°方向,距离A -1海里的B处有一艘走私船,在A处北偏西75°的方向,距A为2海里的C处的缉私船奉命以10
-1海里的B处有一艘走私船,在A处北偏西75°的方向,距A为2海里的C处的缉私船奉命以10 ≈2.449)
≈2.449)