题目内容
(14题和15题二选一,选涂填题号,再做题.)
以直角坐标系的原点为极点,x轴的正半轴为极轴,并在两种坐标系中取相同的长度单位,已知直线的极坐标方程为θθθ=
(p∈R),它与曲线
相交于两点A和B,则|AB|=______.
以直角坐标系的原点为极点,x轴的正半轴为极轴,并在两种坐标系中取相同的长度单位,已知直线的极坐标方程为θθθ=
| π |
| 4 |
|
∵ρ=
,
利用ρcosθ=x,ρsinθ=y,进行化简
∴x-y=0
相消去α可得
圆的方程(x-1)2+(y-2)2=4得到圆心(1,2),半径r=2,
所以圆心(1,2)到直线的距离d=
=
,
所以|AB|=2
=
∴线段AB的长为
故答案为:
.
| π |
| 4 |
利用ρcosθ=x,ρsinθ=y,进行化简
∴x-y=0
|
圆的方程(x-1)2+(y-2)2=4得到圆心(1,2),半径r=2,
所以圆心(1,2)到直线的距离d=
| 2 | ||
|
| 2 |
所以|AB|=2
| r2-d2 |
| 14 |
∴线段AB的长为
| 14 |
故答案为:
| 14 |

练习册系列答案
相关题目
 (p∈R),它与曲线
(p∈R),它与曲线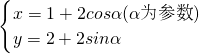 相交于两点A和B,则|AB|=________.
相交于两点A和B,则|AB|=________.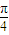 (p∈R),它与曲线
(p∈R),它与曲线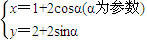 相交于两点A和B,则|AB|= .
相交于两点A和B,则|AB|= . 长AB和DC相交于点P. 若PB=2,PD=6,则
长AB和DC相交于点P. 若PB=2,PD=6,则 的值为 。
的值为 。